
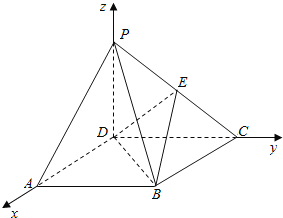
【题目】如图,四棱锥P—ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.

(Ⅰ)证明PA//平面BDE;
(Ⅱ)求二面角B—DE—C的平面角的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)证明见解析.
;(Ⅲ)证明见解析.
【解析】
(Ⅰ)以D为坐标原点,分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,利用向量法能证明PA∥平面BDE;(Ⅱ)由已知求出平面BDE的一个法向量和平面DEC的一个法向量,利用向量法能求出二面角B﹣DE﹣C的余弦值;(Ⅲ)由已知得PB⊥DE,假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=
,(0<λ∠1),由此利用向量法能求出在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.
(Ⅰ)证明:以D为坐标原点,
分别以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,
设PD=DC=2,则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0),
![]() =(2,0,﹣2),
=(2,0,﹣2),![]() =(0,1,1),
=(0,1,1),![]() ,
,
设![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
则由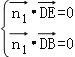 ,得
,得![]() ,
,
取y=﹣1,得![]() .
.
∵![]() =2﹣2=0,∴
=2﹣2=0,∴![]() ,
,
又PA不包含于平面BDE,PA∥平面BDE;
(Ⅱ)由(Ⅰ)知![]() =(1,﹣1,1)是平面BDE的一个法向量,
=(1,﹣1,1)是平面BDE的一个法向量,
又![]() =
=![]() =(2,0,0)是平面DEC的一个法向量.
=(2,0,0)是平面DEC的一个法向量.
设二面角B﹣DE﹣C的平面角为θ,
∴cosθ=cos<![]() ,
,![]() >=
>=![]() .
.
故二面角B﹣DE﹣C的余弦值为![]() .
.
(Ⅲ)∵![]() =(2,2,﹣2),
=(2,2,﹣2),![]() =(0,1,1),
=(0,1,1),
∴![]() =0,∴PB⊥DE,
=0,∴PB⊥DE,
假设棱PB上存在点F,使PB⊥平面DEF,设![]() ,(0<λ∠1),
,(0<λ∠1),
则![]() =(2λ,2λ,﹣2λ),
=(2λ,2λ,﹣2λ),![]() =
=![]() =(2λ,2λ,2﹣2λ),
=(2λ,2λ,2﹣2λ),
由![]() =0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
=0,得4λ2+4λ2﹣2λ(2﹣2λ)=0,
∴![]() ∈(0,1),此时PF=
∈(0,1),此时PF=![]() ,
,
即在棱PB上存在点F,PF=![]() ,使得PB⊥平面DEF.
,使得PB⊥平面DEF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱ABC-A1B1C1中,CA=4,CB=4,CC1=2![]() ,∠ACB=90°,点M在线段A1B1上.
,∠ACB=90°,点M在线段A1B1上.

(1)若A1M=3MB1,求异面直线AM和A1C所成角的余弦值;
(2)若直线AM与平面ABC1所成角为30°,试确定点M的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了调查高一年级学生的体育锻炼情况,从甲、乙、丙3个班中,按分层抽样的方法获得了部分学生一周的锻炼时间(单位:h),数据如下,
甲 | 6 | 6.5 | 7 | 7.5 | 8 | |||
乙 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
丙 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | 12 | 13.5 |
(1)求三个班中学生人数之比;
(2)估计这个学校高一年级学生中,一周的锻炼时间超过10h的百分比;
(3)估计这个学校高一年级学生一周的平均锻炼时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为两个随机事件,给出以下命题:(1)若
为两个随机事件,给出以下命题:(1)若![]() 为互斥事件,且
为互斥事件,且![]() ,
,![]() ,则
,则![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(3)若
为相互独立事件;(3)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(4)若
为相互独立事件;(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(5)若
为相互独立事件;(5)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;其中正确命题的个数为( )
为相互独立事件;其中正确命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读:
已知![]() 、
、![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
解法如下:![]() ,
,
当且仅当![]() ,即
,即![]() 时取到等号,
时取到等号,
则![]() 的最小值为
的最小值为![]() .
.
应用上述解法,求解下列问题:
(1)已知![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)已知![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)已知正数![]() 、
、![]() 、
、![]() ,
,![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次人才招聘会上,假定某毕业生赢得甲公司面试机会的概率为![]() ,赢得乙、丙两公司面试机会的概率均为
,赢得乙、丙两公司面试机会的概率均为![]() ,且三家公司是否让其面试是相互独立的,则该毕业生只赢得甲、乙两家公司面试机会的概率为( )
,且三家公司是否让其面试是相互独立的,则该毕业生只赢得甲、乙两家公司面试机会的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com