练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体中，点，分别为棱，的中点，点为上底面的中心，过，，三点的平面把正方体分为两部分，其中含的部分为，不含的部分为，连结和的任一点，设与平面所成角为，则的最大值为

    A. B.

    C. D.

    【答案】B

    【解析】

    连结.可证平行四边形即为截面. 五棱柱为，三棱柱为，设点为的任一点，过点作底面的垂线，垂足为，连结，则即为与平面所成的角，所以.

    进而得到的最大值.

    连结.因为平面.所以过的平面与平面的交线一定是过点且与平行的直线.过点作交于点，交于点，则，连结，.则平行四边形即为截面.则五棱柱为，三棱柱为，设点为的任一点，过点作底面的垂线，垂足为，连结，则即为与平面所成的角，所以.

    因为，要使的正弦值最大，必须最大，最小，当点与点重合时符合题意.故.故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣x；

    （1）求函数f（x）的解析式；

    （2）求不等式f（x）＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第82页第8题的函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：

    ①同学甲发现：函数的定义域为；

    ②同学乙发现：函数是偶函数；

    ③同学丙发现：对于任意的都有；

    ④同学丁发现：对于任意的，都有；

    ⑤同学戊发现：对于函数定义域中任意的两个不同实数，总满足.

    其中所有正确研究成果的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年8月18日，举世瞩目的第18届亚运会在印尼首都雅加达举行，为了丰富亚运会志愿者的业余生活，同时鼓励更多的有志青年加入志愿者行列，大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛（满分120分）并计划对成绩前15名的志愿者进行奖励，现将所有志愿者的竞赛成绩制成频率分布直方图，如图所示，若第三组与第五组的频数之和是第二组的频数的3倍，试回答以下问题：

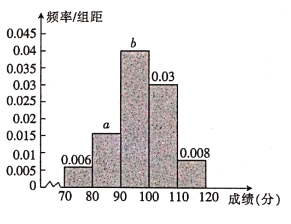
    （1）求图中的值；

    （2）求志愿者知识竞赛的平均成绩；

    （3）从受奖励的15人中按成绩利用分层抽样抽取5人，再从抽取的5人中，随机抽取2人在主会场服务，求抽取的这2人中其中一人成绩在分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于的方程， ，分别求满足下列条件实数的取值范围：

    （1）有解；

    （2）有唯一解；

    （3）有两个解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的一条弦被点平分，则此弦所在的直线方程是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）（江苏省南京师大附中2018届高三高考考前模拟考试数学试题）已知等差数列{an}和等比数列{bn}均不是常数列，若a1＝b1＝1，且a1，2a2，4a4成等比数列， 4b2，2b3，b4成等差数列．

    （1）求{an}和{bn}的通项公式；

    （2）设m，n是正整数，若存在正整数i，j，k（i＜j＜k），使得ambj，amanbi，anbk成等差数列，求m＋n的最小值；

    （3）令cn＝，记{cn}的前n项和为Tn，{ }的前n项和为An．若数列{pn}满足p1＝c1，且对n≥2, n∈N*，都有pn＝＋Ancn，设{pn}的前n项和为Sn，求证：Sn＜4＋4lnn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的中心在原点，焦点F1，F2在坐标轴上，离心率为，且过点．点M(3，m)在双曲线上．

    (1)求双曲线的方程；

    (2)求证：；

    (3)求△F1MF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“日行一万步，健康你一生”的养生观念已经深入人心，由于研究性学习的需要，某大学生收集了手机“微信运动”团队中特定甲、乙两个班级名成员一天行走的步数，然后采用分层抽样的方法按照，，，分层抽取了名成员的步数，并绘制了如下尚不完整的茎叶图（单位：千步）；已知甲、乙两班行走步数的平均值都是千步.

    （1）求，的值；

    （2）若估计该团队中一天行走步数少于千步的人数比处于千步的人数少人，求的值.

    查看答案和解析>>

    同步练习册答案