
【题目】定义在R上的奇函数f(x)对任意x∈R都有f(x)=f(x+4),当x∈(﹣2,0)时,f(x)=2x , 则f(2016)﹣f(2015)= .
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点. 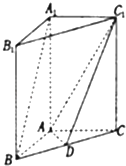
(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() △
△![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为边
分别为边![]() 的中点,点
的中点,点![]() 分别为线段
分别为线段![]() 的中点.将△
的中点.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() .点
.点![]() 为线段
为线段![]() 上的一点,如图2.
上的一点,如图2.
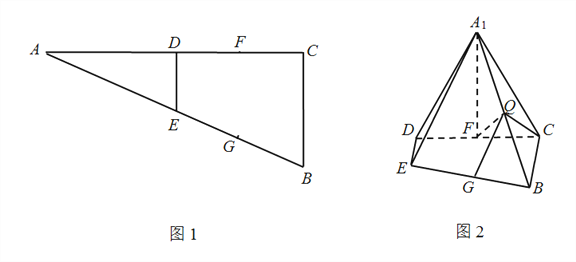
(Ⅰ)求证: ![]() ;
;
(Ⅱ)线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由;
的长,若不存在,请说明理由;
(Ⅲ)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,已知
中,已知![]() 对任意
对任意![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .(这里
.(这里![]() 均为实数)
均为实数)
(1)若![]() 是等差数列,求
是等差数列,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() ;
;
(3)是否存在实数![]() ,使数列
,使数列![]() 是公比不为
是公比不为![]() 的等比数列,且任意相邻三项
的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列?若存在,求出所有
按某顺序排列后成等差数列?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的序号是 .
①函数y=ax(a>0且a≠1)与函数 ![]() (a>0且a≠1)的定义域相同;
(a>0且a≠1)的定义域相同;
②函数y=k3x(k>0)(k为常数)的图象可由函数y=3x的图象经过平移得到;
③函数 ![]() (x≠0)是奇函数且函数
(x≠0)是奇函数且函数 ![]() (x≠0)是偶函数;
(x≠0)是偶函数;
④若x1是函数f(x)的零点,且m<x1<n,则f(m)f(n)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,x∈(﹣2,2)
,x∈(﹣2,2)
(1)判断f(x)的奇偶性并说明理由;
(2)求证:函数f(x)在(﹣2,2)上是增函数;
(3)若f(2+a)+f(1﹣2a)>0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为实数集R,A={x|3≤x<7},B={x| ![]() ≤2x≤8},C={x|x<a}.
≤2x≤8},C={x|x<a}.
(1)求R(A∪B)
(2)如果A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益函数为R(x)= 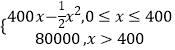 ,其中x是仪器的产量(单位:台);
,其中x是仪器的产量(单位:台);
(1)将利润f(x)表示为产量x的函数(利润=总收益﹣总成本);
(2)当产量x为多少台时,公司所获利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com