已知圆C:(x-4)2+y2=4,圆D的圆心D在y轴上,且与圆C外切,圆D交y轴于A、B两点(A在B的上方),点P为(-3,0).
(1)若D(0,3),求∠APB的正切值;
(2)若D在y轴上运动,当D在何位置时,tan∠APB最大?并求出最大值;
(3)在x轴上是否存在点Q,使当D在y轴上运动时,∠AQB为定值?如果存在,求出点Q的坐标;如果不存在,请说明理由.
解:(1)由圆C:(x-4)
2+y
2=4,知C(4,0),圆C的半径为2.…(1分)
又圆C与圆D外切,D(0,3),
∴
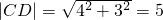
,圆D的半径R=5-2=3,…(3分)
而圆D截y轴于(0,6)、(0,0)两点,不妨设A(0,6),B(0,0)
∴tan∠APB=
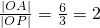
. …(4分)
(2)当D在y轴上运动时,令D(0,t),
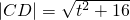
,
圆D的半径R=
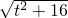
-2,A(0,t+R),B(0,t-R),…(5分)
∠APB=∠APC-∠BPC,
∴tan∠APB=
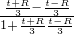
…(7分)
=
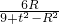
=

=
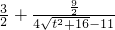
…(8分)
≤
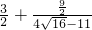
=
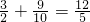
…(9分)
当D为(0,0)时,tan∠APB最大,最大值为

; …(10分)
(3)设Q(x,0),所以可得tan∠AQB=
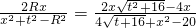
为常数
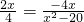
,…(11分)
即

或
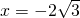
或x=0. …(12分)
但当x=0时,若A、B分别在x轴两旁时,∠AQB=180°,
若A、B都在x轴同旁时,∠AQB=0°,故x=0不合题意,舍去.
所以,存在满足题意的点Q为(

,0)或(-

,0).…(14分)
分析:(1)由已知中圆C:(x-4)
2+y
2=4,点D(0,3),可求出CD的长,进而求出圆D的半径,求出A,B两点坐标后,即可求得∠APB的正切值;
(2)设D点坐标为(0,t),可以求出对应的圆D的半径和A,B两点的坐标,进而求出∠APB正切的表达式,求出其最值后,再根据正切函数的单调性,求出∠APB的最大值;
(3)假设存在点Q(x,0),根据∠AQB是定值,我们构造关于x的方程,若方程有解,则存在这样的点,若方程无实根,则不存在这样的点.
点评:本题重点考查直线和圆的方程的应用,考查直线的倾斜角与斜率,考查正切函数的单调性,考查存在性问题,有综合性.

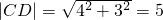 ,圆D的半径R=5-2=3,…(3分)
,圆D的半径R=5-2=3,…(3分)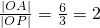 . …(4分)
. …(4分)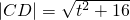 ,
,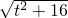 -2,A(0,t+R),B(0,t-R),…(5分)
-2,A(0,t+R),B(0,t-R),…(5分)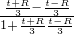 …(7分)
…(7分)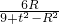 =
= =
=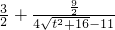 …(8分)
…(8分)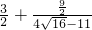 =
=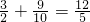 …(9分)
…(9分) ; …(10分)
; …(10分)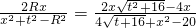 为常数
为常数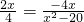 ,…(11分)
,…(11分) 或
或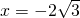 或x=0. …(12分)
或x=0. …(12分) ,0)或(-
,0)或(- ,0).…(14分)
,0).…(14分)
