
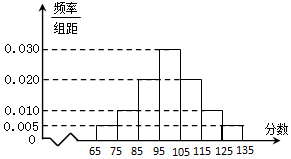
 ijУ�߶��꼶��һ����ѧ����������ȡ�˲���ѧ������ѧ�ɼ����һ���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
ijУ�߶��꼶��һ����ѧ����������ȡ�˲���ѧ������ѧ�ɼ����һ���������õ�����Ƶ�ʷֲ�ֱ��ͼ������ ��1����ͬһ�������ø�����е�ֵ��Ϊ����������ƽ������ʽ�ͷ��ʽ�������ȡ������ƽ����x����������s2��
��2�����ɣ�1��֪��X��N��100��210�����Ӷ�P��X��129��=P��X��100+2��14.5�����ɵý��ۣ�
���ɢ�֪����β��飬��У�߶�1000��ѧ���У��ɼ���12��9�֣����ϵ�����ԼΪ1000��0.0228��
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ��֪��$\overline{x}=��70��0.005+80��0.010+90��0.020+100��0.030+110��0.020+120��0.010$+130��0.005����10=100�� ����3�֣�
s2=��-30��2��0.005��10+��-20��2��0.010��10+��-10��2��0.020��10+0��0.030��10+102��0.020��10+202��0.010��10+302��0.005��10=210����6�֣�
��2�����ɣ�1��֪��X��N��100��210����
�Ӷ�P��X��129��=P��X��100+2��14.5��=$\frac{1-P��100-2��14.5��X��100+2��14.5��}{2}$=$\frac{1-0.9544}{2}$=0.0228
����10�֣�
���ɢ�֪����β��飬��У�߶�1000��ѧ���У��ɼ���12��9�֣����ϵ�����ԼΪ1000��0.0228=22.8��23�ˡ���12�֣�
���� ���⿼������ƽ����x����������s2����������̬�ֲ������е��⣬


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��b��c | B�� | a��c��b | C�� | c��a��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{3}$ | B�� | $\frac{5}{3}$ | C�� | 5 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ǰ������½��۴��� | B�� | Сǰ������½��۴��� | ||
| C�� | ������ʽ�����½��۴��� | D�� | ����û�����⣬������ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��1] | B�� | [1��2] | C�� | [-1��2�� | D�� | ��-1��2�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com