【题目】为了了解某校九年级1 600名学生的体能情况，随机抽查了部分学生，测试1分钟仰卧起坐的成绩(次数)，将数据整理后绘制成如图所示的频率分布直方图，根据直方图的数据，下列结论错误的是( )
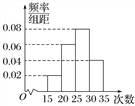
A. 该校九年级学生1分钟仰卧起坐的次数的中位数为26.25
B. 该校九年级学生1分钟仰卧起坐的次数的众数为27.5
C. 该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人
D. 该校九年级学生1分钟仰卧起坐的次数少于20次的约有32人
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案科目：高中数学 来源： 题型：
【题目】一个四棱锥的三视图如图所示，关于这个四棱锥，下列说法正确的是（ ）
A. 最长的棱长为
B. 该四棱锥的体积为
C. 侧面四个三角形都是直角三角形
D. 侧面三角形中有且仅有一个等腰三角形
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点。
(Ⅰ)求椭圆C的方程；
(Ⅱ)是否存在平行于OA的直线
，使得直线
与椭圆C有公共点，且直线OA与
的距离等于4？若存在，求出直线
的方程；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C： 
，过点
的直线l的参数方程为：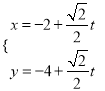 
(t为参数)，直线l与曲线C分别交于M、N两点．
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程；
(Ⅱ)若| PM |，| MN |，| PN |成等比数列，求a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知x与y之间的几组数据如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得的线性回归方程为
＝
x＋
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y＝b′x＋a′，则以下结论正确的是( )
A. 
>b′，
>a′ B. >b′，<a′
C. <b′，>a′ D. <b′，<a′
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
（
）的图象为
， 
关于点
的对称的图象为
， 
对应的函数为
．
（Ⅰ）求函数
的解析式，并确定其定义域；
（Ⅱ）若直线
与
只有一个交点，求
的值，并求出交点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设方程2x＋x＋2＝0和方程log2x＋x＋2＝0的根分别为p和q，函数f(x)＝(x＋p)·(x＋q)＋2，则( )
A. f(2)＝f(0)<f(3) B. f(0)<f(2)<f(3)
C. f(3)<f(0)＝f(2) D. f(0)<f(3)<f(2)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“双十一”期间，某淘宝店主对其商品的上架时间
（分钟）和销售量
（件）的关系作了统计，得到如下数据：
经计算： 
， 
， 
， 
.
（1）该店主通过作散点图，发现上架时间与销售量线性相关，请你帮助店主求出上架时间与销售量的线性回归方程（保留三位小数），并预测商品上架1000分钟时的销售量；
（2）从这11组数据
中任选2组，设
且
的数据组数为
，求
的分布列与数学期望.
附：线性回归方程公式：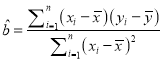 
， 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有2人去淘宝网购物的概率;
(2)求这4个人中去淘宝网购物的人数大于去京东商城购物的人数的概率:
(3)用X,Y分别表示这4个人中去淘宝网购物的人数和去京东商城购物的人数,记
,求随机变量
的分布列与数学期望
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
