
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
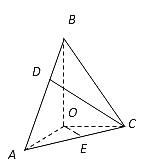
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
【答案】(1)![]() .(2)D在AB的中点时.
.(2)D在AB的中点时.
【解析】
(1)由题意的BO⊥平面ACO,即BO就是三棱锥B﹣ACO的高,然后根据体积建立等式关系,解之即可求出所求;
(2)以O为原点,OA为x轴,OC为y轴,OB为z轴,建立空间直角坐标系,设D(x,0,![]() (1﹣x)),设
(1﹣x)),设![]() 和
和![]() 的夹角为θ,则coaθ
的夹角为θ,则coaθ![]() 建立等式关系,解之即可求出x的值,从而可判定点D的位置.
建立等式关系,解之即可求出x的值,从而可判定点D的位置.
(1)由题意的BO⊥平面ACO,即BO就是三棱锥B﹣ACO的高,
在Rt△ABO中,设AO=a,∠BAO=60°,所以BO![]() a,
a,
CO=a,所以VB﹣ACO![]() AO×BO×CO
AO×BO×CO![]() a3
a3![]() .
.
所以a=1,所以三棱锥的高BO为![]() .
.
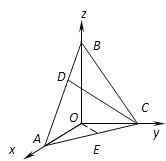
(2)以O为原点,如图建立空间直角坐标系,
设D(x,0,![]() (1﹣x)),则C(0,1,0),E(
(1﹣x)),则C(0,1,0),E(![]() ,
,![]() ,0 )
,0 )
![]() (﹣x,1,
(﹣x,1,![]() ( x﹣1)),
( x﹣1)),![]() (
(![]() ,
,![]() ,0),
,0),
设![]() 和
和![]() 的夹角为θ
的夹角为θ
则coaθ![]()
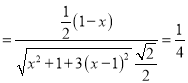 ,
,
解之得,x=2(舍去)或x![]() ,
,
所以当D在AB的中点时,![]() 和
和![]() 的夹角大小为arccos
的夹角大小为arccos![]() .
.


科目:高中数学 来源: 题型:
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中国北京世界园艺博览会期间,某工厂生产
中国北京世界园艺博览会期间,某工厂生产![]() 、
、![]() 、
、![]() 三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
纪念品 | 纪念品 | 纪念品 | |
精品型 |
|
|
|
普通型 |
|
|
|
现采用分层抽样的方法在这一天生产的纪念品中抽取![]() 个,其中
个,其中![]() 种纪念品有
种纪念品有![]() 个.
个.
(1)求![]() 的值;
的值;
()从![]() 种精品型纪念品中抽取
种精品型纪念品中抽取![]() 个,其某种指标的数据分别如下:
个,其某种指标的数据分别如下:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,把这
,把这![]() 个数据看作一个总体,其均值为
个数据看作一个总体,其均值为![]() ,方差为
,方差为![]() ,求
,求![]() 的值;
的值;
(3)用分层抽样的方法在![]() 种纪念品中抽取一个容量为
种纪念品中抽取一个容量为![]() 的样木,从样本中任取
的样木,从样本中任取![]() 个纪念品,求至少有
个纪念品,求至少有![]() 个精品型纪念品的概率.
个精品型纪念品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与
与![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
![]() 求点M的轨迹C的方程;
求点M的轨迹C的方程;
![]() 设N是圆E:
设N是圆E:![]() 上位于第四象限的一点,过N作圆E的切线
上位于第四象限的一点,过N作圆E的切线![]() ,与曲线C交于A,B两点
,与曲线C交于A,B两点![]() 求证:
求证:![]() 的周长为10.
的周长为10.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com