
已知函数
 为常数,
为常数,
(1)当 时,求函数
时,求函数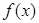 在
在 处的切线方程;
处的切线方程;
(2)当 在
在 处取得极值时,若关于
处取得极值时,若关于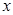 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)若对任意的 ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围。
的取值范围。
(1)  (2)
(2) 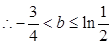
(3) 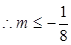
【解析】
试题分析:(1)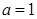 时,
时,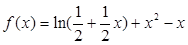
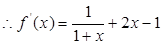 ,于是
,于是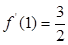 ,又
,又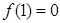 ,即切点为(
,即切点为(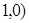
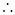 切线方程为
切线方程为 —————————————————————————5分
—————————————————————————5分
(2)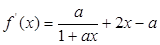 ,
,
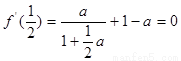 ,即
,即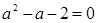 ,
,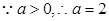
此时,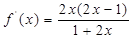 ,
,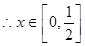 上减,
上减, 上增,
上增,
又
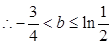 ———————————————————————————10分
———————————————————————————10分
(3)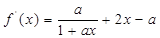
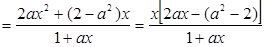
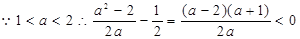 ,即
,即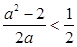 (
(
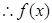 在
在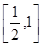 上增,
上增,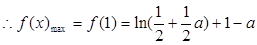
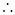 只须
只须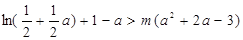 ————————————————12分
————————————————12分
(法一)设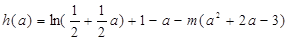
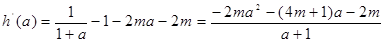
又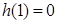
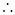
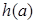 在1的右侧需先增,
在1的右侧需先增,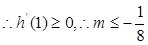
设 ,对称轴
,对称轴
又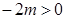 ,
,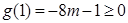
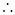 在
在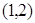 上,
上,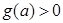 ,即
,即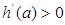
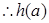 在
在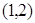 上单调递增,
上单调递增,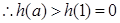
即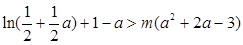 ,
,
于是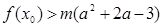
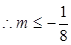 ——————————————————-15分
——————————————————-15分
(法二)
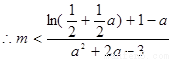
设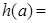
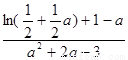 ,
,
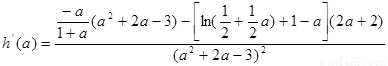
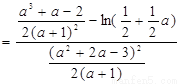
设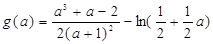 ,
,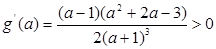
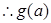 在
在 上增,又
上增,又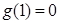 ,
,
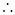
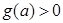 ,即
,即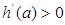 ,
,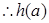 在
在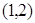 上增
上增
又
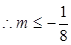
数学 选修1B模块答案
题号:03答案
(1)法一:由柯西不等式知:

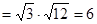 ——————————————————5分
——————————————————5分
法二: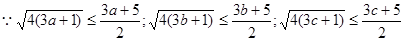
相加得: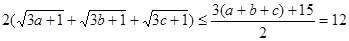
 ——————————————————————5分
——————————————————————5分
法三:令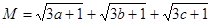
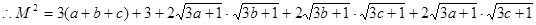
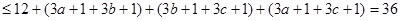
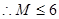 —————————————————————————————————5分
—————————————————————————————————5分
(2)由柯西不等式得:
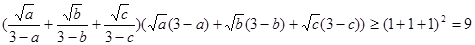
又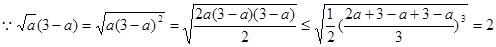
此时,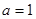 时取“=”号;同理:
时取“=”号;同理: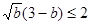 ,
, .
.
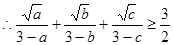 ,所以,当
,所以,当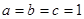 时,
时, 的最小值为
的最小值为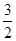
(提示:本题也可以用基本不等式求解:如: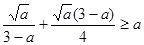 ,其中
,其中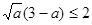 也可以构造函数
也可以构造函数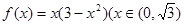 用导数求最大值)—————————10分
用导数求最大值)—————————10分
题号:04答案
(1)直线
令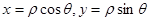 代入直线方程得:
代入直线方程得:
 直线
直线 的极坐标方程为:
的极坐标方程为: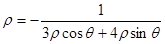 .————————————3分
.————————————3分
(写成 的形式不扣分)
的形式不扣分)
(2)(i)曲线C的普通方程为: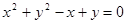 ————————————4分
————————————4分
直线L的参数方程的标准形式为: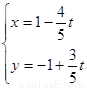 ——————————————5分
——————————————5分
联立得: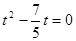 ,
,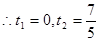 ;
; ———————————7分
———————————7分
(ii)设AB中点为M对应的参数为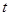 ,则
,则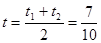 ,
,
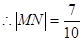 —————————————————————————————10分
—————————————————————————————10分
考点:导数,极值,不等式
点评:对于导数在研究函数中的问题,主要考查两个方面,一个是几何意义的运用,一个就是判定函数单调性,属于中档题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年湖北省高三(上)期末数学试卷(文科)(解析版) 题型:解答题
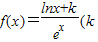 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省徐州市诚贤中学高三(上)第二次质量检测数学试卷(解析版) 题型:解答题
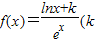 为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省数学选修1-2模块考试数学试卷(解析版) 题型:解答题
已知函数 为常数)
为常数)
(1)若 上单调递增,且
上单调递增,且
(2)若f(x)在x=1和x=3处取得极值,且在x∈[-6,6]时,函数 的图象在直线
的图象在直线
的下方,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012届福建省泉州市高三上学期期中文科数学试卷 题型:解答题
已知函数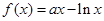 .(
.(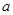 为常数)
为常数)
(1)当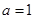 时,求函数
时,求函数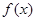 的最小值;
的最小值;
(2)求函数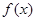 在
在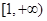 上的最值;
上的最值;
(3)试证明对任意的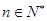 都有
都有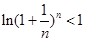
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期末考试理科数学试卷 题型:解答题
(本小题14分)已知函数 为常数.
为常数.
(1)求函数 的定义域
的定义域 ;
;
(2)若 时, 对于
时, 对于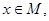 比较
比较 与
与 的大小;
的大小;
(3)若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com