
已知函数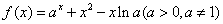 .
.
(Ⅰ)当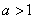 时,求证:函数
时,求证:函数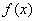 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数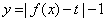 有三个零点,求
有三个零点,求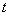 的值;
的值;
(Ⅲ)若存在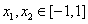 ,使得
,使得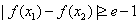 ,试求
,试求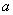 的取值范围.
的取值范围.
解:(Ⅰ)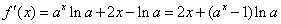 …………………………………3分
…………………………………3分
由于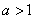 ,故当
,故当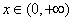 时,
时,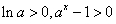 ,所以
,所以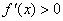 ,
,
故函数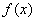 在
在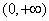 上单调递增
……………………………………………………………5分
上单调递增
……………………………………………………………5分
(Ⅱ)当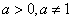 时,因为
时,因为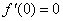 ,且
,且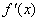 在R上单调递增,
在R上单调递增,
故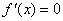 有唯一解
有唯一解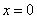 ……………………………………………………………………7分
……………………………………………………………………7分
所以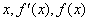 的变化情况如下表所示:
的变化情况如下表所示:
|
x |
|
0 |
|
|
|
- |
0 |
+ |
|
|
递减 |
极小值 |
递增 |
又函数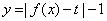 有三个零点,所以方程
有三个零点,所以方程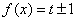 有三个根,
有三个根,
而 ,所以
,所以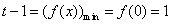 ,解得
,解得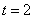 ……………………………11分
……………………………11分
(Ⅲ)因为存在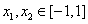 ,使得
,使得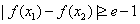 ,
,
所以当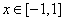 时,
时,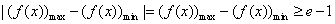 …………12分
…………12分
由(Ⅱ)知,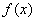 在
在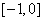 上递减,在
上递减,在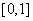 上递增,
上递增,
所以当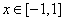 时,
时,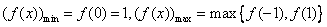 ,
,
而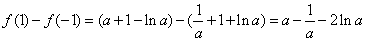 ,
,
记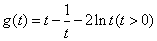 ,因为
,因为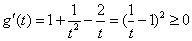 (当
(当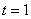 时取等号),
时取等号),
所以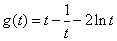 在
在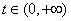 上单调递增,而
上单调递增,而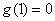 ,
,
所以当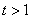 时,
时,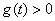 ;当
;当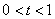 时,
时,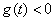 ,
,
也就是当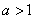 时,
时,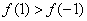 ;当
;当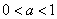 时,
时,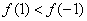 ………………………14分
………………………14分
①当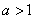 时,由
时,由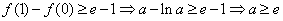 ,
,
②当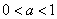 时,由
时,由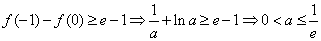 ,
,
综上知,所求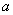 的取值范围为
的取值范围为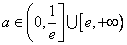 …………………………………………16分
…………………………………………16分
数学附加题部分


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com