
【题目】如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=![]() ,
,![]() .
.

(1)求证:CF⊥平面BDE;
(2)求二面角A-BE-D的大小。
【答案】(1)见证明;(2) ![]() (或
(或![]() )
)
【解析】
(1)连接FG,可证得四边形CEFG为菱形,故得![]() .再根据平面ABCD
.再根据平面ABCD![]() 平面ACEF得到
平面ACEF得到![]() 平面ACEF,从而
平面ACEF,从而![]() .由线面垂直的判定定理可得结论成立.(2)建立空间直角坐标系,求出平面BDE和平面ABE的法向量,求出两向量的夹角的余弦值并结合图形可得所求角的大小.
.由线面垂直的判定定理可得结论成立.(2)建立空间直角坐标系,求出平面BDE和平面ABE的法向量,求出两向量的夹角的余弦值并结合图形可得所求角的大小.
(1)连接FG,
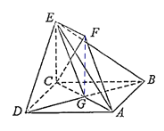
∵![]() ,
,
∴四边形CEFG为菱形,
∴![]() .
.
∵ABCD为正方形,
∴![]() ,
,
又平面ABCD![]() 平面ACEF,平面ABCD
平面ACEF,平面ABCD![]() 平面ACEF=AC,BD
平面ACEF=AC,BD![]() 平面ABCD
平面ABCD
∴![]() 平面ACEF,
平面ACEF,
∵CF![]() 平面ACEF,
平面ACEF,
∴![]() .
.
又![]() ,BD
,BD![]() 平面BDE, BG
平面BDE, BG![]() 平面BDE,
平面BDE,
∴![]() 平面BDE.
平面BDE.
(1)∵正方形ABCD和四边形ACEF所在的平面互相垂直,且CE⊥AC,
∴CE⊥平面ABCD,
以C为原点,CB为![]() 轴,CD为
轴,CD为![]() 轴,CE为
轴,CE为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
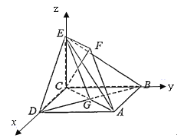
则![]() ,
,
∴![]() ,
,![]() ,
,
由(1)可得![]() 是平面BDE的一个法向量.
是平面BDE的一个法向量.
设平面ABE的一个法向量为![]()
由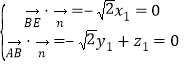 ,得
,得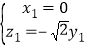 ,
,
令![]() ,得
,得![]() ,
,
∴![]() ,
,
由图形可得二面角A-BE-D为锐角,
∴二面角A-BE-D的大小为![]() (或
(或![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A. 若直线a,b与平面α所成角都是30°,则这两条直线平行
B. 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C. 若直线a,b平行,则这两条直线中至少有一条与平面α平行
D. 若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量![]() ,
,![]() ,令函数
,令函数![]() ,若函数
,若函数![]() 的部分图象如图所示,且点
的部分图象如图所示,且点![]() 的坐标为
的坐标为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求函数![]() 的单调增区间及对称轴方程;
的单调增区间及对称轴方程;
(3)若把方程![]() 的正实根从小到大依次排列为
的正实根从小到大依次排列为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() ,射线
,射线![]() 与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A,B两点(异于M).
与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A,B两点(异于M).
(1)求证:直线AB的斜率为定值;
(2)求![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高一学生暑假里在家读书情况,特随机调查了50名男生和50名女生平均每天的阅读时间(单位:分钟),统计如下表:

(1)根据统计表判断男生和女生谁的平均读书时间更长?并说明理由;
(2)求100名学生每天读书时间的平均数,并将每天平均时间超过和不超过平均数的人数填入下列的列联表:

(3)根据(2)中列联表,能否有99%的把握认为“平均阅读时间超过或不超过平均数是否与性别有关?”
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() . 在以坐标原点为极点,
. 在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ) 写出圆 ![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
( Ⅱ ) 设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;![]() .
.
(2)![]() .
.
【解析】【试题分析】(I)利用圆心和半径,写出圆的参数方程,将圆的极坐标方程展开后化简得直角坐标方程.(II)求得![]() 两点的坐标, 设点
两点的坐标, 设点![]() ,代入向量
,代入向量![]() ,利用三角函数的值域来求得取值范围.
,利用三角函数的值域来求得取值范围.
【试题解析】
(Ⅰ)圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)由直线![]() 的方程
的方程![]() 可得点
可得点![]() ,点
,点![]() .
.
设点![]() ,则
,则![]()
![]() .
.
![]()
![]() .
.
由(Ⅰ)知![]() ,则
,则![]()
![]()
![]() .
.
因为![]() ,所以
,所以![]() .
.
【题型】解答题
【结束】
23
【题目】选修4-5:不等式选讲
已知函数![]() ,
, ![]() .
.
(Ⅰ)若对于任意![]() ,
, ![]() 都满足
都满足![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com