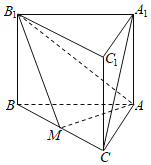
【题目】如图，直三棱柱ABC﹣A1B1C1，中，点M是棱BC的中点.
（2）求证：A1C∥平面AB1M；
（2）如果AB＝AC，求证AM⊥平面BCC1B1.
【答案】（1）见解析；（2）见解析
【解析】
（1）连结A1B，交AB1于M，连结MN，在三角形
中由中位线定理证得，线线平行，由线面平行的判定定理得证；
（2）由等腰三角形三线合一证得AM⊥BC，由直三棱柱证得BB1⊥底面ABC，进而证得AM⊥BB1，由线面垂直的判定定理得证.
（1）连结A1B，交AB1于M，连结MN，
∵直三棱柱ABC﹣A1B1C1中，点M是棱BC的中点.
∴N是A1B的中点，∴MN∥A1C，
∵MN平面AB1M，A1C平面AB1M，
∴A1C∥平面AB1M.
（2）∵AB＝AC，M是BC中点，
∴AM⊥BC，
∵直三棱柱ABC﹣A1B1C1中，BB1⊥底面ABC，AM平面ABC，
∴AM⊥BB1，
∵BC∩BB1＝B，∴AM⊥平面BCC1B1.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】己知函数
.
（1)若f（x）有两个极值点，求实数m的取值范围：
(2)若函数
有且只有三个不同的零点，分别记为x1，x2，x3，设x1＜x2＜x3，且
的最大值是e2，求x1x3的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线
（
，
），
，
是双曲线的两个顶点，
是双曲线上的一点，且与点在双曲线的同一支上，关于
轴的对称点是
，若直线
，
的斜率分别是
，
，且
，则双曲线的离心率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市地铁项目正在紧张建设中，通车后将给市民出行带来便利.已知某条线路通车后，地铁的发车时间间隔
（单位：分钟）满足
.经测算，地铁载客量与发车时间间隔相关，当
时地铁为满载状态，载客量为
人，当
时，载客量会减少，减少的人数与
的平方成正比，且发车时间间隔为
分钟时的载客量为
人，记地铁载客量为
.
（1）求的表达式，并求当发车时间间隔为
分钟时，地铁的载客量；
（2）若该线路每分钟的净收益为
（元），问当发车时间间隔为多少时，该线路每分钟的净收益最大？每分钟的最大净收益为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【题目】已知抛物线C：y2＝2x，过点(2,0)的直线l交C于A，B两点，圆M是以线段AB为直径的圆．
(1)证明：坐标原点O在圆M上；
(2)设圆M过点P(4，－2)，求直线l与圆M的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在箱子中有10个小球，其中有3个红球，3个白球，4个黑球．从这10个球中任取3个．求：
（1）取出的3个球中红球的个数
的分布列；
（2）取出的3个球中红球个数多于白球个数的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
