
【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
【答案】见解析
【解析】(1)因为f(x)=(-x2+x-1)ex,
所以f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex.
所以曲线f(x)在点(1,f(1))处的切线斜率为
k=f′(1)=-2e.
又f(1)=-e,
所以所求切线方程为y+e=-2e(x-1),即2ex+y-e=0.
(2)因为f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex,
当x<-1或x>0时,f′(x)<0;
当-1<x<0时,f′(x)>0,
所以f(x)=(-x2+x-1)ex在(-∞,-1)上单调递减,在(-1,0)上单调递增,在(0,+∞)上单调递减,
所以f(x)在x=-1处取得极小值f(-1)=-![]() ,在x=0处取得极大值f(0)=-1.
,在x=0处取得极大值f(0)=-1.
令g(x)=![]() x3+
x3+![]() x2+m,得g′(x)=x2+x.
x2+m,得g′(x)=x2+x.
当x<-1或x>0时,g′(x)>0;
当-1<x<0时,g′(x)<0,
所以g(x)在(-∞,-1)上单调递增,在(-1,0)上单调递减,在(0,+∞)上单调递增.
故g(x)在x=-1处取得极大值g(-1)=![]() +m,在x=0处取得极小值g(0)=m.
+m,在x=0处取得极小值g(0)=m.
因为方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,
x2+m有3个不同的根,
即函数f(x)与g(x)的图象有3个不同的交点,
所以![]() ,即
,即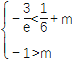 .
.
所以-![]() -
-![]() <m<-1.
<m<-1.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盐化某厂决定采用以下方式对某块盐池进行开采:每天开采的量比上一天减少![]() ,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的
,10天后总量变为原来的一半,为了维持生态平衡,剩余总量至少要保留原来的![]() ,已知到今天为止,剩余的总量是原来的
,已知到今天为止,剩余的总量是原来的![]() .
.
(1)求![]() 的值;
的值;
(2)到今天为止,工厂已经开采了几天?
(3)今后最多还能再开采多少天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .现提供
.现提供![]() 的大致图像的8个选项:
的大致图像的8个选项:
(A)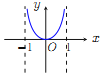 (B)
(B)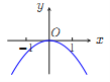 (C)
(C) (D)
(D)
(E) (F)
(F)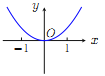 (G)
(G)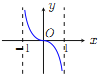 (H)
(H)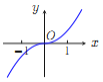
(Ⅰ)请你作出选择,你选的是( );
(Ⅱ)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决下列问题:
①![]() 的定义域是 ;
的定义域是 ;
②就奇偶性而言, ![]() 是 ;
是 ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】做投掷2个骰子试验,用(x,y)表示点P的坐标,其中x表示第1个骰子出现的点数,y表示第2个骰子出现的点数.
(1)求点P在直线y=x上的概率.
(2)求点P不在直线y=x+1上的概率.
(3)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:
类别 | 文艺节目 | 新闻节目 | 总计 |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,则大于40岁的观众应该抽取几名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com