
【题目】(本题满分16分)已知![]() ,
,![]() ,
,![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 是常数列,
是常数列,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]()
![]() ,求证:对任意的
,求证:对任意的![]() ,数列
,数列![]() 单调递减.
单调递减.
【答案】(1)![]() ;(2)详见解析;(3)详见解析;
;(2)详见解析;(3)详见解析;
【解析】
试题(1)由已知条件可化得数列![]() 的前
的前![]() 和,再作差求得通项,要注意分类讨论;(2)与(1)的思路相同,利用和作差,得到项之间的关系式,进而表示出数列
和,再作差求得通项,要注意分类讨论;(2)与(1)的思路相同,利用和作差,得到项之间的关系式,进而表示出数列![]() 的通项,利用等差数列的定义进行证明,还应注意补充说明
的通项,利用等差数列的定义进行证明,还应注意补充说明![]() ;(3)由(2)中和作差后的通项间的关系式可推得
;(3)由(2)中和作差后的通项间的关系式可推得![]() 与
与![]() 的关系式,则证得从第2项起
的关系式,则证得从第2项起![]() 成等比数列,求得其通项公式,同时也求得数列
成等比数列,求得其通项公式,同时也求得数列![]() 从第二项起是等差数列,所以从第2项起
从第二项起是等差数列,所以从第2项起![]() 为差比数列,通过作差或作商可以研究它的单调性;
为差比数列,通过作差或作商可以研究它的单调性;
试题解析:(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为数列![]() 是各项不为零的常数列,所以
是各项不为零的常数列,所以![]() ,
,![]() ,
,
则由![]() 及
及![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
当![]() 时,
时,![]() ,也满足
,也满足![]() ,故
,故![]() .
.
(2)因为![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
即![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以当![]() 时,
时,![]() ,两式相减得
,两式相减得![]()
![]() ,
,
所以数列![]() 从第二项起是公差为
从第二项起是公差为![]() 等差数列;
等差数列;
又当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
故数列![]() 是公差为
是公差为![]() 等差数列.
等差数列.
(3)由(2)得当![]() 时,
时,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
即![]() ,故从第二项起数列
,故从第二项起数列![]() 是等比数列,
是等比数列,
所以当![]() 时,
时,![]() ,
,
![]() ,
,
另外由已知条件得![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,因而
,因而![]() ,令
,令![]()
![]() ,则
,则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以对任意的
,所以对任意的![]() ,数列
,数列![]() 单调递减.
单调递减.


科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和
的前n项和![]() ,且满足
,且满足![]() ,
,![]() ,数列
,数列![]() 是首项为2,公比为q(
是首项为2,公比为q(![]() )的等比数列.
)的等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设正整数k,t,r成等差数列,且![]() ,若
,若![]() ,求实数q的最大值;
,求实数q的最大值;
(3)若数列![]() 满足
满足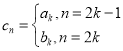 ,
,![]() ,其前n项和为
,其前n项和为![]() ,当
,当![]() 时,是否存在正整数m,使得
时,是否存在正整数m,使得![]() 恰好是数列
恰好是数列![]() 中的项?若存在,求岀m的值;若不存在,说明理由.
中的项?若存在,求岀m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,过焦点且与
,过焦点且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() ,过点
,过点![]() 的任意一条直线
的任意一条直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划,该地扶贫办统计了2018年![]() 位农民的年收人并制成如下频率分布直方图:
位农民的年收人并制成如下频率分布直方图:
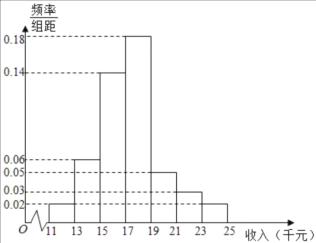
(1)根据频率分布直方图,估计![]() 位农民的年平均收入
位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求:
.利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了![]() 位农民。若每个农民的年收人相互独立,问:这
位农民。若每个农民的年收人相互独立,问:这![]() 位农民中的年收入不少于
位农民中的年收入不少于![]() 千元的人数最有可能是多少?
千元的人数最有可能是多少?
附:参考数据与公式![]()
则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com