
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}e$ | C. | e | D. | 2e |
分析 通过参数分离,利用基本不等式放缩可知问题转化为2lna≤$\frac{3+{e}^{x-4}}{x}$在x>0时恒成立,记g(x)=$\frac{3+{e}^{x-4}}{x}$,二次求导并结合单调性可知当x=4时g(x)取得最小值g(4)=1,进而计算即得结论.
解答 解:设f(x)=ex+y-4+ex-y+4+6,
不等式4xlna≤ex+y-4+ex-y+4+6恒成立,即为不等式4xlna≤f(x)恒成立.
即有f(x)=ex(ey-4+e-(y-4))+6≥6+2ex(当且仅当ey-4=e-(y-4),即y=0时,取等号),
由不等式ex+y-4+ex-y+4+6≥4xlna恒成立,只需要4xlna≤6+2ex-4,
即有2lna≤$\frac{3+{e}^{x-4}}{x}$在x>0时恒成立,
令g(x)=$\frac{3+{e}^{x-4}}{x}$,g′(x)=$\frac{{e}^{x-4}(x-1)-3}{{x}^{2}}$,令g′(x)=0,即(x-1)ex-4=3,
令h(x)=(x-1)ex-4,(x>0),h′(x)=xex-4>0,
∵x>0,ex-4>0,
∴h′(x)>0,∴h(x)在(0,+∞)上单调递增,
又∵h(4)=3,即有(x-1)ex-4=3的根为4,
∴当x>4时g(x)递增,当0<x<4时g(x)递减,
∴当x=4时,g(x)取得最小值g(4)=1,
∴2lna?1,lna?$\frac{1}{2}$,
∴0<a?$\sqrt{e}$,(当x=2,y=0时,a取得最大值$\sqrt{e}$),
故选A.
点评 本题考查不等式恒成立问题注意转化为求函数的最值问题,运用参数分离和构造函数运用导数判断单调性是解题的关键,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4,-6,3 | B. | -4,6,3 | C. | -4,-6,3 | D. | 4,-6,-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | [1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
省农科站要检测某品牌种子的发芽率,计划采用随机数表法从该品牌800粒种子中抽取60粒进行检测,现将这800粒种子编号如下001,002,…,800,若从随机数表第8行第7列的数7开始向右读,则所抽取的第4粒种子的编号是( ).(下表是随机数表第7行至第9行)

A.105 B.507 C.071 D.717
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
如图, ABCD-A1B1C1D1为正方体,下面结论错误的是( ).
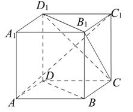
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1角为60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com