
【题目】已知函数 ![]() ,若满足f(1)=
,若满足f(1)= ![]()
(1)求实数a的值;
(2)证明:f(x)为奇函数.
(3)判断并证明函数f(x)的单调性.
【答案】
(1)解:f(1)= ![]() ;
;
∴ ![]() ;
;
∴a=1
(2)解:证明: ![]() ;
;
该函数定义域为R,f(﹣x)= ![]() ;
;
∴f(x)为奇函数
(3)解: ![]() ,可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:
,可看出x增大时,f(x)增大,∴f(x)在R上为增函数,证明如下:
设x1,x2∈R,且x1<x2,则:
![]() =
= ![]() ;
;
∵x1<x2;
∴ ![]() ,
, ![]() ;
;
∴f(x1)<f(x2);
∴f(x)在R上为增函数
【解析】(1)根据f(1)= ![]() 便可求出a=1;(2)写出
便可求出a=1;(2)写出 ![]() ,定义域显然为R,容易得到f(﹣x)=﹣f(x),从而得出该函数为奇函数;(3)分离常数得到
,定义域显然为R,容易得到f(﹣x)=﹣f(x),从而得出该函数为奇函数;(3)分离常数得到 ![]() ,根据单调性定义便可判断该函数在R上单调递增,根据增函数的定义证明:设任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根据指数函数的单调性证明f(x1)<f(x2)即可得出f(x)在R上单调递增.
,根据单调性定义便可判断该函数在R上单调递增,根据增函数的定义证明:设任意的x1 , x2∈R,且x1<x2 , 然后作差,通分,根据指数函数的单调性证明f(x1)<f(x2)即可得出f(x)在R上单调递增.
【考点精析】利用函数单调性的判断方法和函数奇偶性的性质对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】如图,正方形ADEF与梯形ABCD所在的闰面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
(2)求平面BEC与平面ADEF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)设函数h(x)=g(x)﹣f(x),求函数h(x)在区间[2,4]上的值域;
(2)定义min(p,q)表示p,q中较小者,设函数H(x)=min{f(x),g(x)}(x>0), ①求函数H(x)的单调区间及最值;
②若关于x的方程H(x)=k有两个不同的实根,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,其左顶点
,其左顶点![]() 在圆
在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (点
(点![]() 与点
与点![]() 不重合),且直线
不重合),且直线![]() 与
与![]() 轴的交于点
轴的交于点![]() ,试问
,试问![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ) 当a=0时,求曲线f(x)在x =1处的切线方程;
(Ⅱ) 设函数![]() ,求函数h(x)的极值;
,求函数h(x)的极值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一点x0,使得
在[1,e](e=2.718 28…)上存在一点x0,使得![]() 成立,求a的取值范围.
成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如下表:
评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
评分类型 | D | C | B | A |
 考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
考核评估后,对各连锁店的评估分数进行统计分析,得其频率分布直方图如下:
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 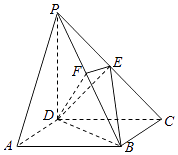
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①乘积(a+b+c+d)(p+q+r)(m+n)展开式的项数是24;
②由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是36;
③某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为24;
④已知(1+x)8=a0+a1x+…+a8x8 , 其中a0 , a1 , …,a8中奇数的个数为2.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论: ①已知函数f(x)是定义在R上的奇函数,若f(﹣1)=2,f(﹣3)=﹣1,则f(3)<f(﹣1);
②函数y=log ![]() (x2﹣2x)的单调递增减区间是(﹣∞,0);
(x2﹣2x)的单调递增减区间是(﹣∞,0);
③已知函数f(x)是奇函数,当x≥0时,f(x)=x2 , 则当x<0时,f(x)=﹣x2;
④若函数y=f(x)的图象与函数y=ex的图象关于直线y=x对称,则对任意实数x,y都有f(xy)=f(x)+f(y).
则正确结论的序号是(请将所有正确结论的序号填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com