
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】计算:
(1)[(5 ![]() )0.5+(0.008)﹣
)0.5+(0.008)﹣ ![]() ÷(0.2)﹣1]÷0.06250.25;
÷(0.2)﹣1]÷0.06250.25;
(2)[(1﹣log63)2+log62log618]÷log64.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,函数f(x)=lg(4﹣x)﹣ ![]() 的定义域为集合A,集合B={x|﹣2<x<a}.
的定义域为集合A,集合B={x|﹣2<x<a}.
(1)求集合UA;
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,双曲线
,双曲线![]() :
: ![]() ,若以
,若以![]() 的长轴为直径的圆与
的长轴为直径的圆与![]() 的一条渐近线交于A、B两点,且椭圆
的一条渐近线交于A、B两点,且椭圆![]() 与该渐近线的两交点将线段AB三等分,则
与该渐近线的两交点将线段AB三等分,则![]() 的离心率是( )
的离心率是( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a﹣ ![]() 为奇函数.
为奇函数.
(1)求a的值;
(2)试判断函数f(x)在(﹣∞,+∞)上的单调性,并证明你的结论;
(3)若对任意的t∈R,不等式f[t2﹣(m﹣2)t]+f(t2﹣m+1)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌茶壶的原售价为80元/个,今有甲、乙两家茶具店销售这种茶壶,甲店用如下方法促销:如果只购买一个茶壶,其价格为78元/个;如果一次购买两个茶壶,其价格为76元/个;…,一次购买的茶壶数每增加一个,那么茶壶的价格减少2元/个,但茶壶的售价不得低于44元/个;乙店一律按原价的75%销售.现某茶社要购买这种茶壶x个,如果全部在甲店购买,则所需金额为y1元;如果全部在乙店购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)该茶社去哪家茶具店购买茶壶花费较少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
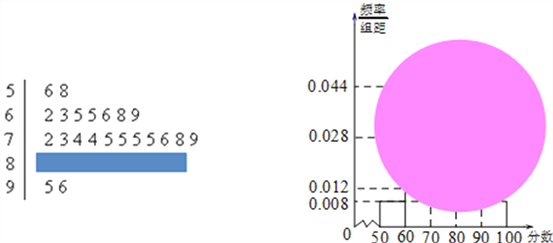
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com