Question

20．过椭圆一个焦点F的直线与椭圆交于两点P、Q，A₁、A₂为椭圆长轴上的顶点，A₁P和A₂Q交于点M，A₂P和A₁Q交于点N，则MF⊥NF．

Answer 1

分析 设椭圆的标准方程为：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）．F（-c，0）．设PQ的方程为：my=x+c．P（x₁，y₁），Q（x₂，y₂），不妨设y₁＞y₂．与椭圆方程联立化为（b²m²+a²）y²-2mcb²y-b⁴=0．直线A₂P的方程为：$y=\frac{{y}_{1}}{{x}_{1}-a}（x-a）$，直线A₁Q的方程为：y=$\frac{{y}_{2}}{{x}_{2}+a}（x+a）$，联立解得x=$\frac{a[2m{y}_{1}{y}_{2}-c（{y}_{1}+{y}_{2}）+a（{y}_{1}-{y}_{2}）]}{-c（{y}_{1}-{y}_{2}）+a（{y}_{1}+{y}_{2}）}$，利用根与系数的关系可得：y₁-y₂=$\sqrt{（{y}_{1}+{y}_{2}）^{2}-4{y}_{1}{y}_{2}}$．可得x=$-\frac{{a}^{2}}{c}$．即直线A₂P与直线A₁Q的交点N在椭圆的左准线l：x=-$\frac{{a}^{2}}{c}$上．同理可得：A₁P和A₂Q交于点M也在椭圆的左准线l：x=-$\frac{{a}^{2}}{c}$上．下面证明：$\overrightarrow{MF}⊥\overrightarrow{NF}$．利用$\overrightarrow{MF}•\overrightarrow{NF}$=0即可．

解答 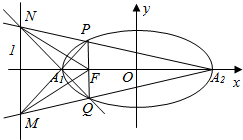证明：设椭圆的标准方程为：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）．F（-c，0）．
设PQ的方程为：my=x+c．P（x₁，y₁），Q（x₂，y₂），不妨设y₁＞y₂．
联立$\left\{\begin{array}{l}{my=x+c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$，化为（b²m²+a²）y²-2mcb²y-b⁴=0．
∴y₁+y₂=$\frac{2mc{b}^{2}}{{b}^{2}{m}^{2}+{a}^{2}}$，y₁y₂=$\frac{-{b}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}$．
直线A₂P的方程为：$y=\frac{{y}_{1}}{{x}_{1}-a}（x-a）$，
直线A₁Q的方程为：y=$\frac{{y}_{2}}{{x}_{2}+a}（x+a）$，
联立解得x=$\frac{a[{y}_{1}{x}_{2}+{y}_{2}{x}_{1}+a（{y}_{1}-{y}_{2}）]}{{y}_{1}{x}_{2}-{y}_{2}{x}_{1}+a（{y}_{1}+{y}_{2}）}$=$\frac{a[2m{y}_{1}{y}_{2}-c（{y}_{1}+{y}_{2}）+a（{y}_{1}-{y}_{2}）]}{-c（{y}_{1}-{y}_{2}）+a（{y}_{1}+{y}_{2}）}$，
y₁-y₂=$\sqrt{（{y}_{1}+{y}_{2}）^{2}-4{y}_{1}{y}_{2}}$=$\frac{2a{b}^{2}\sqrt{1+{m}^{2}}}{{b}^{2}{m}^{2}+{a}^{2}}$．
分子u=a$[\frac{-{2mb}^{4}}{{b}^{2}{m}^{2}+{a}^{2}}-\frac{2m{c}^{2}{b}^{2}}{{b}^{2}{m}^{2}+{a}^{2}}$+$\frac{2{a}^{2}{b}^{2}\sqrt{{m}^{2}+1}}{{b}^{2}{m}^{2}+{a}^{2}}]$，
分母v=-$\frac{2ac{b}^{2}\sqrt{{m}^{2}+1}}{{b}^{2}{m}^{2}+{a}^{2}}$+$\frac{2mca{b}^{2}}{{b}^{2}{m}^{2}+{a}^{2}}$．
∴x=$\frac{u}{v}$=$-\frac{{a}^{2}}{c}$．
∴直线A₂P与直线A₁Q的交点N在椭圆的左准线l：x=-$\frac{{a}^{2}}{c}$上．
同理可得：A₁P和A₂Q交于点M也在椭圆的左准线l：x=-$\frac{{a}^{2}}{c}$上．
下面证明：$\overrightarrow{MF}⊥\overrightarrow{NF}$．
${y}_{1}^{2}$=${b}^{2}（1-\frac{{x}_{1}^{2}}{{a}^{2}}）$=$\frac{{b}^{2}（{a}^{2}-{x}_{1}^{2}）}{{a}^{2}}$．
$\overrightarrow{MF}•\overrightarrow{NF}$=$（\frac{{a}^{2}}{c}-c）^{2}$+y_My_N
=$\frac{{b}^{4}}{{c}^{2}}$+$\frac{{y}_{1}^{2}}{{x}_{1}^{2}-{a}^{2}}$$（\frac{{a}^{4}}{{c}^{2}}-{a}^{2}）$
=$\frac{{b}^{4}}{{c}^{2}}$-$\frac{{b}^{2}}{{a}^{2}}$×$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$=0．
∴$\overrightarrow{MF}⊥\overrightarrow{NF}$．
∴MF⊥NF．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、向量垂直与数量积的关系，考查了推理能力与计算能力，属于难题．