
分析 根据条件便可得到f(0)=0,f(x)在(0,2]上单调递减,从而可以得出x>0时,f(x)<0,而x<0时,f(x)>0,并且由原不等式得到f(1-x)<f(x).这样可将x分成:-2≤x≤0,0<x<1,和1≤x≤2这几种情况,然后根据f(1-x),f(x)的符号,和f(x)的单调性便可求得每种情况下原不等式的解,求并集便可得出原不等式的解集.
解答 解:根据f(x)在[-2,2]上为奇函数,在[-2,0]上单调递减;
∴f(x)在[-2,2]上单调递减;
∴由f(1-x)+f(-x)<0得,f(1-x)<f(x);
∴$\left\{\begin{array}{l}{-2≤1-x≤2}\\{-2≤x≤2}\\{1-x>x}\end{array}\right.$;
解得$-1≤x<\frac{1}{2}$;
∴原不等式的解集为$[-1,\frac{1}{2})$.
故答案为:[-1,$\frac{1}{2}$).
点评 考查奇函数的定义,奇函数f(x)在原点有定义时,f(0)=0,奇函数在对称区间上的单调性,以及减函数定义的运用.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,-1] | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,2) | C. | (-∞,2] | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
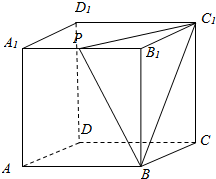 如图,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作截面PBC1平行的截面,则该截面的面积为( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作截面PBC1平行的截面,则该截面的面积为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com