
分析 (1)利用抛物线y2=2px(p>0)经过点M(2,4),可得抛物线的方程,即可求出椭圆的焦点,利用椭圆的离心率e=$\frac{1}{2}$,求出a,b,即可得出椭圆的方程;
(2)设切线l的斜率为k,则切线l的方程为y=k(x+2),带入抛物线方程,利用判别式等于0,即可得出结论.
解答 解:(1)∵抛物线y2=2px(p>0)经过点M(2,4),
∴42=2p×2,解得p=4,…(2分)
∴抛物线的标准方程为y2=8x.…(3分)
∴抛物线的焦点为(2,0),即椭圆的焦点为F1(-2,0),F2(2,0),即c=2. …(4分)
又∵椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,∴a=4,b=2$\sqrt{3}$,…(6分)
∴椭圆的标准方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.…(7分)
(2)由题意知切线l的斜率存在,设切线l的斜率为k,则切线l的方程为y=k(x+2).…(8分)
由$\left\{\begin{array}{l}{y=k(x+2)}\\{{y}^{2}=8x}\end{array}\right.$消去y,得方程k2x2+(4k2-8)x+4k2=0.…(10分)
∵l与抛物线相切,∴△=(4k2-8)2-4k2•4k2=0,∴k=±1,…(12分)
∴切线l的方程为y=x+2或y=-x-2.…(14分)
点评 本题考查抛物线、椭圆的方程与性质,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
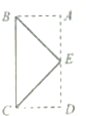 如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.
如图,矩形ABCD中,E为AD的中点,AB=1,BC=2,连接EB,EC,若△BEC绕直线AD旋转一周,则所形成的几何体的表面积为(4+2$\sqrt{2}$)π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,图象关于直线x=$\frac{π}{3}$对称.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,图象关于直线x=$\frac{π}{3}$对称.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
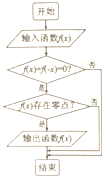 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数:| A. | f(x)=sinx | B. | f(x)=cosx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=log2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com