
【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
【答案】解析
【解析】(1)当a=2时,f(x)=x2-2x+ln(x+1),
f′(x)=2x-2+![]() =
=![]() .
.
令f′(x)=0,得x=±![]() .
.
当x∈![]() 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当x∈![]() 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
当x∈![]() 时,f′(x)>0,f(x)单调递增.
时,f′(x)>0,f(x)单调递增.
所以函数f(x)的极大值点为x=-![]() ,极小值点为x=
,极小值点为x=![]() .
.
(2)因为f′(x)=2x-a+![]() ,
,
由f′(x)>x,得2x-a+![]() >x,
>x,
所以由题意知,a<x+![]() (0<x<1)恒成立.
(0<x<1)恒成立.
又x+![]() =x+1+
=x+1+![]() -1≥1,当且仅当x+1=
-1≥1,当且仅当x+1=![]() ,即x=0时等号成立.
,即x=0时等号成立.
所以a≤1.
故所求实数a的取值范围为(-∞,1].
(3)证明:①当n=1时,c2=f′(c1)=2c1-a+![]() .
.
因为c1>0,所以c1+1>1,又a<1,
所以c2-c1=c1-a+![]() =c1+1+
=c1+1+![]() -(a+1)>2-(a+1)=1-a>0,
-(a+1)>2-(a+1)=1-a>0,
所以c2>c1,即当n=1时结论成立.
②假设当n=k(k∈N*,k≥1)时结论成立,即ck+1>ck>0,
当n=k+1时,
ck+2-ck+1=ck+1-a+![]() =ck+1+1+
=ck+1+1+![]() -(a+1)>2-(a+1)=1-a>0.
-(a+1)>2-(a+1)=1-a>0.
所以ck+2>ck+1,即当n=k+1时结论成立.
由①②知数列{cn}是单调递增数列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
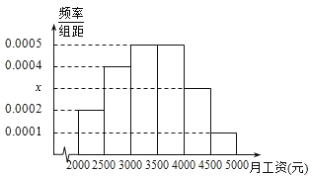
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 的两条对角线
的两条对角线![]() 相交于
相交于![]() ,现用五种颜色(其中一种为红色)对图中四个三角形
,现用五种颜色(其中一种为红色)对图中四个三角形![]() 进行染色,且每个三角形用一种颜色图染.
进行染色,且每个三角形用一种颜色图染.
(1)若必须使用红色,求四个三角形![]() 中有且只有一组相邻三角形同色的染色方法的种数;
中有且只有一组相邻三角形同色的染色方法的种数;
(2)若不使用红色,求四个三角形![]() 中所有相邻三角形都不同色的染色方法的种数.
中所有相邻三角形都不同色的染色方法的种数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
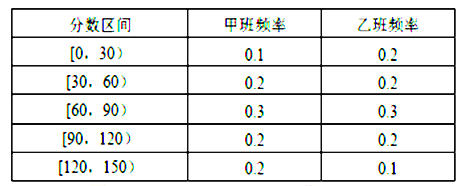
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
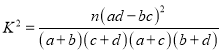 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P
=1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P![]() .
.
(1)求椭圆C的离心率;
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且![]() =
=![]() +
+![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了![]() ,
, ![]() ,
, ![]() ,
, ![]() 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是![]() ,3号门里是
,3号门里是![]() ;乙同学说:2号门里是
;乙同学说:2号门里是![]() ,3号门里是
,3号门里是![]() ;丙同学说:4号门里是
;丙同学说:4号门里是![]() ,2号门里是
,2号门里是![]() ;丁同学说:4号门里是
;丁同学说:4号门里是![]() ,3号门里是
,3号门里是![]() .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某电子商务平台的调查统计显示,参与调查的1 000位上网购物者的年龄情况如图所示.
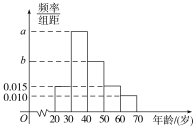
(1)已知[30,40),[40,50),[50,60)三个年龄段的上网购物者人数成等差数列,求a,b的值;
(2)该电子商务平台将年龄在[30,50)内的人群定义为高消费人群,其他年龄段的人群定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放100元的代金券,现采用分层抽样的方式从参与调查的1 000位上网购物者中抽取10人,并在这10人中随机抽取3人进行回访,求此3人获得代金券总和X(单位:元)的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-1|+|x-2a|.
(1)当a=1时,求f(x)≤3的解集;
(2)当x∈[1,2]时,f(x)≤3恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 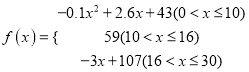 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com