
分析 判断一个函数的奇偶性,需先求函数的定义域,定义域若关于原点对称,再判断f(-x)和f(x)的关系,从而由奇函数、偶函数的定义得出该函数的奇偶性,而若定义域不关于原点对称,则该函数非奇非偶,根据这个方法去判断这三个函数的奇偶性即可.
解答 解:(1)该函数定义域为R;
f(-x)=|-x+1|+|-x-1|=|x-1|+|x+1|=f(x);
∴f(x)为偶函数;
(2)解1-|x|≥0得,-1≤x≤1;
∴该函数的定义域为[-1,1];
g(-x)=$-x\sqrt{1-|x|}=-g(x)$;
∴该函数为奇函数;
(3)该函数定义域为{x|x≠1};
定义域不关于原点对称;
∴该函数非奇非偶.
点评 考查奇函数、偶函数的定义,判断一个函数奇偶性的方法和过程,注意需先求函数的定义域.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
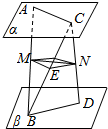 如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.
如图,设平面α∥平面β,AB、CD是两异面直线,且A、C∈α,B、D∈β,AC⊥BD,AC=6,BD=8,M是AB的中点,过点M作一个平面γ,交CD于N,交BC于E,且γ∥α∥β,求线段MN的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos0°<cos$\frac{1}{2}$<cos1<cos30°<cosπ° | B. | cos0°<cosπ°<cos$\frac{1}{2}$cos30°<cos1 | ||
| C. | cos0°>cos$\frac{1}{2}$>cos1>cos30°>cosπ° | D. | cos0°>cosπ°>cos$\frac{1}{2}$>cos30°>cos1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com