
| 分类 | 患呼吸道疾病 | 未患呼吸道疾病 | 合计 |
| 户外作业人员 | 40 | 60 | 100 |
| 非户外作业人员 | 60 | 240 | 300 |
| 合计 | 100 | 300 | 400 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 0.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)确定基本事件的情况,即可求出相应的概率;
(2)求出K2,与临界值比较,即可得出结论.
解答 解:(1)∵四个专家组选取的城市可以相同,也可以不同,且每个城市都必须由专家组选取,
∴不同的选取方法有${C}_{3}^{1}{C}_{4}^{2}{A}_{2}^{2}$=36种方法,
A城市恰有两名专家组选取方法有12种,故概率为$\frac{1}{3}$;
(2)K2=$\frac{400(40×240-60×60)^{2}}{100×300×100×300}$=16>6.635,
∴有超过99%的把握认为“户外作业”与“患有呼吸道疾病”有关.
点评 本题考查概率的计算,考查独立性检验知识的运用,正确计算是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,0) | B. | (0,3) | C. | $(\sqrt{3},0)$ | D. | $(0,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 2月1日 | 2月2日 | 2月3日 | 2月4日 | 2月5日 |
| 温差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 发芽数x(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
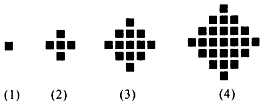 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com