
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 的取值仅能是2;(3)详见解析.
的取值仅能是2;(3)详见解析.
【解析】
试题(1)由数组的极差的定义,可知,![]() ,这时三数为
,这时三数为![]() ,第二次操作后,
,第二次操作后,![]() ,这时三数为
,这时三数为![]() ,第三次操作后,
,第三次操作后,![]() ,,这时三数为
,,这时三数为![]() ,第四次操作后,
,第四次操作后,![]() ,这时三数为
,这时三数为![]() ,第五次操作后,
,第五次操作后,![]() ,这时三数为
,这时三数为![]() ,第六次操作后,
,第六次操作后,![]() ,这时三数为
,这时三数为![]() ,
,![]() ,第2014次操作后,
,第2014次操作后,![]() ,这时三数为
,这时三数为![]() ;(2)已知
;(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,这时极差
,这时极差![]() 最小值为
最小值为![]() ,当
,当![]() 时,这时
时,这时![]() 是三个连续的正整数,即为
是三个连续的正整数,即为![]() ,由(1)可知,通过变化后,所得数仍然是
,由(1)可知,通过变化后,所得数仍然是![]() ,所以数组的极差不会改变,即
,所以数组的极差不会改变,即![]() ,符合题意,当
,符合题意,当![]() ,这时
,这时![]() 三个数,通过变化成
三个数,通过变化成![]() ,这是极差为
,这是极差为![]() ,或
,或![]() ,这样就可以确定出
,这样就可以确定出![]() 的取值仅能是2;(3)若
的取值仅能是2;(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() ,这时
,这时![]() 三数形式为
三数形式为![]() ,由二项式定理可知
,由二项式定理可知![]() ,故所以
,故所以![]() 的极差
的极差![]() 是3的倍数,这样根据极差的定义,通过操作,得到
是3的倍数,这样根据极差的定义,通过操作,得到![]() 是一个公差为
是一个公差为![]() 的等差数列,从而可得出结论.
的等差数列,从而可得出结论.
(1)![]() ,
,![]() ,
,![]() 3分
3分
(2)法一:
①当![]() 时,则
时,则![]()
所以![]() ,
,![]() ,
,
由操作规则可知,每次操作,数组中的最大数![]() 变为最小数
变为最小数![]() ,最小数
,最小数![]() 和次
和次
小数![]() 分别变为次小数
分别变为次小数![]() 和最大数
和最大数![]() ,所以数组的极差不会改变.
,所以数组的极差不会改变.
所以,当![]() 时,
时,![]() 恒成立.
恒成立.
②当![]() 时,则
时,则![]()
所以![]() 或
或![]()
所以总有![]() .
.
综上讨论,满足![]() 的
的![]() 的取值仅能是2. 8分
的取值仅能是2. 8分
法二:
因为![]() ,所以数组
,所以数组![]() 的极差
的极差![]()
所以![]() ,
,
若![]() 为最大数,则
为最大数,则![]()
若![]() ,则
,则![]()
若![]() ,则
,则![]() ,
,
当![]() 时,可得
时,可得![]() ,即
,即![]()
由![]() 可得
可得![]()
所以![]()
将![]() 代入
代入![]() 得
得![]()
所以当![]() 时,
时,![]() (
(![]() )
)
由操作规则可知,每次操作,数组中的最大数![]() 变为最小数
变为最小数![]() ,最小数
,最小数![]() 和次小
和次小
数![]() 分别变为次小数
分别变为次小数![]() 和最大数
和最大数![]() ,所以数组的极差不会改变.
,所以数组的极差不会改变.
所以满足![]() 的
的![]() 的取值仅能是2. 8分
的取值仅能是2. 8分
(3)因为![]() 是以4为公比的正整数等比数列的三项,
是以4为公比的正整数等比数列的三项,
所以![]() 是形如
是形如![]() (其中
(其中![]() )的数,
)的数,
又因为![]()
所以![]() 中每两个数的差都是3的倍数.
中每两个数的差都是3的倍数.
所以![]() 的极差
的极差![]() 是3的倍数. 9分
是3的倍数. 9分
法1:设![]() ,不妨设
,不妨设![]() ,
,
依据操作![]() 的规则,当在三元数组
的规则,当在三元数组![]() (
(![]() ,
,![]() )中,总满足
)中,总满足![]() 是唯一最大数,
是唯一最大数,![]() 是最小数时,一定有
是最小数时,一定有![]() ,解得
,解得![]() .
.
所以,当![]() 时,
时,![]() .
.
![]() ,
,![]()
依据操作![]() 的规则,当在三元数组
的规则,当在三元数组![]() (
(![]() ,
,![]() )中,总满足
)中,总满足![]() 是最大数,
是最大数,![]() 是最小数时,一定有
是最小数时,一定有![]() ,解得
,解得![]() .
.
所以,当![]() 时,
时,![]() .
.
![]() ,
,![]()
所以存在![]() ,满足
,满足![]() 的极差
的极差![]() . 13分
. 13分
法2:设![]() ,则
,则
①当![]() 中有唯一最大数时,不妨设
中有唯一最大数时,不妨设![]() ,则
,则
![]() ,
,
所以![]()
所以,若![]() 是3的倍数,则
是3的倍数,则![]() 是3的倍数.
是3的倍数.
所以![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
所以![]() 11分
11分
②当![]() 中的最大数有两个时,不妨设
中的最大数有两个时,不妨设![]() ,则
,则
![]() ,
,
所以![]() ,
,
所以,若![]() 是3的倍数,则
是3的倍数,则![]() 是3的倍数.
是3的倍数.
所以![]() ,则
,则![]() ,
,![]()
所以![]() .
.
所以当![]() 时,数列
时,数列![]() 是公差为3的等差数列. 12分
是公差为3的等差数列. 12分
当![]() 时,由上述分析可得
时,由上述分析可得![]() ,此时
,此时![]()
所以存在![]() ,满足
,满足![]() 的极差
的极差![]() . 13分
. 13分


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线
,它的一个焦点与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率为![]() 的直线过点
的直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,设点
两点,设点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过点
过点![]()
![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 的纵截距为
的纵截距为![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
日均浓度 |
|
|
|
|
|
|
空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
空气质量类型 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
甲、乙两城市2013年2月份中的15天对空气质量指数PM2.5进行监测,获得PM2.5日均浓度指数数据如茎叶图所示:
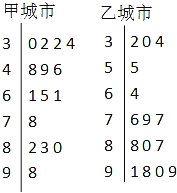
(Ⅰ)根据你所学的统计知识估计甲、乙两城市15天内哪个城市空气质量总体较好?(注:不需说明理由)
(Ⅱ)在15天内任取1天,估计甲、乙两城市空气质量类别均为优或良的概率;
(Ⅲ)在乙城市15个监测数据中任取2个,设X为空气质量类别为优或良的天数,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10日,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:总体平均数为3,中位数为4;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,总体方差为3;
丁地:中位数为2,众数为3;
则甲、乙、两、丁四地中,一定没有发生大规模群体感染的是( )
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com