
【题目】在△ABC中, ![]()
(1)求A的大小;
(2)若a=10,b=8![]() ,求△ABC的面积S.
,求△ABC的面积S.
【答案】(1) ![]() ;(2)8.
;(2)8.
【解析】试题分析:(1)根据正弦定理得到![]() ,将式子变形为
,将式子变形为![]() sin Bcos A=sin(A+C)=sinB,进而得到角A。(2)由余弦定理得到c=14或c=2,再根据面积公式得到结果。
sin Bcos A=sin(A+C)=sinB,进而得到角A。(2)由余弦定理得到c=14或c=2,再根据面积公式得到结果。
解析:
(1)由正弦定理,得![]()
所以![]() sin Bcos A=cos Csin A+sin Ccos A,
sin Bcos A=cos Csin A+sin Ccos A,
即![]() sin Bcos A=sin(A+C)=sinB.
sin Bcos A=sin(A+C)=sinB.
因为B∈(0,π),所以sin B≠0.
所以cos A=![]() .
.
因为A∈(0,π),所以A=![]() .
.
(2)由余弦定理及a=10,b=8![]() ,得
,得
102=(8![]() )2+c2-2×8
)2+c2-2×8![]() ×
×![]() c.
c.
解之得c=14或c=2.
所以S=![]() bcsin A=56或S=
bcsin A=56或S=![]() bcsin A=8.
bcsin A=8.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)若直线![]() 与曲线
与曲线![]() 恰好有一个公共点,求实数
恰好有一个公共点,求实数![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换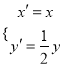 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856263)
已知抛物线y2=2px(p>0)的准线与x轴交于点N,过点N作圆M:(x-2)2+y2=1的两条切线,切点为P、Q,且|PQ|=![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)过抛物线的焦点F作斜率为k1的直线与抛物线交于A、B两点,A、B两点的横坐标均不为2,连接AM,BM并延长分别交抛物线于C、D两点,设直线CD的斜率为k2,问![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月,某国宣布成功进行氢弹试验后,A,B,C,D四国领导人及联合国主席纷纷表示谴责,就此,某电视台特别邀请一军事专家对这一事件进行评论,若该军事专家计划从A,B,C,D四国及联合国主席这5个领导人中任选2人的发言态度进行评论,那么,他评论的这2人中至少包括A、B一国领导人的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856288)
设函数f(x)=aln x-x,g(x)=aex-x,其中a为正实数.
(Ⅰ)若f(x)在(1,+∞)上是单调减函数,且g(x)在(2,+∞)上有最小值,求a的取值范围;
(Ⅱ)若函数f(x)与g(x)都没有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x+1|﹣|2x﹣3|,g(x)=|x+1|+|x﹣a|.
(l)求f(x)≥1的解集;
(2)若对任意的t∈R,s∈R,都有g(s)≥f(t).求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856331)
甲、乙两家快餐店对某日7个时段的光顾的客人人数进行统计并绘制茎叶图如下图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
(Ⅰ)求a,b的值,并计算乙数据的方差;
(Ⅱ)现从乙数据中不大于16的数据中随机抽取两个,求至少有一个数据小于10的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com