
【题目】我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数f(x)与第x天近似地满足f(x)=8+ ![]() (千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(1)求该村的第x天的旅游收入p(x)(单位千元,1≤x≤30,x∈N*)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
【答案】
(1)解:依据题意,有p(x)=f (x)g(x)= ![]() (1≤x≤30,x∈N*)
(1≤x≤30,x∈N*)
= 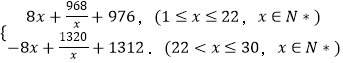
(2)1°当1≤x≤22,x∈N*时,
p(x)=8x+ ![]() +976≥2
+976≥2 ![]() +976=1152(当且仅当x=11时,等号成立),
+976=1152(当且仅当x=11时,等号成立),
因此,p(x)min=p(11)=1152(千元).
2°当22<x≤30,x∈N*时,p(x)= ![]() .
.
求导可得p′(x)<0,所以p(x)= ![]() 在(22,30]上单调递减,
在(22,30]上单调递减,
于是p(x)min=p(30)=1116(千元).
又1152>1116,所以日最低收入为1116千元.
该村两年可收回的投资资金为1116×20%×5%×30×12×2=8035.2(千元)=803.52(万元),
因803.52万元>800万元,所以,该村两年内能收回全部投资资金.
【解析】1、由题意可得 p(x)=f (x)g(x)=![]() ,得到分段函数的解析式。
,得到分段函数的解析式。
2、若以最低日收入的20%作为每一天纯收入的计量依据,并以纯收入的5%的税率收回投资成本,选择合适的解析式第一种情况当1≤x≤22,x∈N*时再根据基本不等式求得最小值当且仅当x=11时,等号成立。第二种情况当22<x≤30,x∈N*时,求导得到p′(x)<0根据单调性在区间(22,30]上单调递减求得最小值1116千元,又1152>1116,所以日最低收入为1116千元,再由1116×20%×5%×30×12×2=8035.2(千元)=803.52(万元),根据实际情况该村两年内能收回全部投资资金。


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x>0时,f(x)=x3+x2 .
(1)求f(x)在R上的解析式;
(2)当x∈[m,n](0<m<n)时,若f(x)的值域为[3m2+2m﹣1,3n2+2n﹣1],求实数m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 经过点
经过点 ![]() ,离心率为
,离心率为 ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(I)求椭圆 ![]() 的方程.
的方程.
(II)若点 ![]() 为椭圆
为椭圆 ![]() 上一动点,点
上一动点,点 ![]() 与点
与点 ![]() 的垂直平分线l交
的垂直平分线l交 ![]() 轴于点
轴于点 ![]() ,求
,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+c,g(x)=aex的图象的一个公共点为P(2,t),且曲线y=f(x),y=g(x)在P点处有相同的切线,若函数f(x)﹣g(x)的负零点在区间(k,k+1)(k∈Z)内,则k= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数x,y满足的约束条件 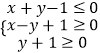 ,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且sinA+ ![]() cosA=2.
cosA=2.
(Ⅰ)求角A的大小;
(Ⅱ)现给出三个条件:①a=2;②B=45°;③c= ![]() b.试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
b.试从中选出两个可以确△ABC的条件,写出你的选择,并以此为依据求△ABC的面积.(只写出一个方案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读材料:根据两角和与差的正弦公式,有: sin(α+β)=sinαcosβ+cosαsinβ﹣﹣﹣﹣﹣﹣①
sin(α﹣β)=sinαcosβ﹣cosαsinβ﹣﹣﹣﹣﹣﹣②
由①+②得sin(α+β)+sin(α﹣β)=2sinαcosβ﹣﹣﹣﹣﹣﹣③
令α+β=A,α﹣β=β 有α= ![]() ,β=
,β= ![]() 代入③得 sinA+sinB=2sin
代入③得 sinA+sinB=2sin ![]() cos
cos ![]() .
.
(1)利用上述结论,试求sin15°+sin75°的值;
(2)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA﹣cosB=﹣2sin ![]() cos
cos ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com