
称满足以下两个条件的有穷数列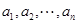 为
为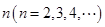 阶“期待数列”:
阶“期待数列”:
①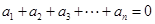 ;②
;②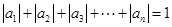 .
.
(1)若等比数列 为
为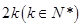 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是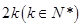 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列” 的前k项和为
的前k项和为 :
:
(i)求证: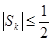 ;
;
(ii)若存在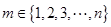 使
使 ,试问数列
,试问数列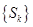 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
(1)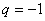 .
.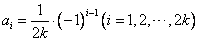 或
或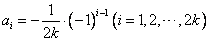 ;
;
(2)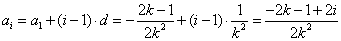 ;
;
(3)(i)证明见解析;(ii)不能,证明见解析.
【解析】
试题分析:(1)数列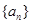 中等比数列,因此
中等比数列,因此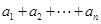 是其前
是其前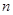 和,故利用前前
和,故利用前前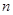 项和公式,分
项和公式,分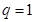 和
和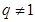 进行讨论,可很快求出
进行讨论,可很快求出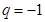 ,
,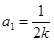 或
或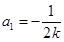 ;(2)
;(2)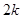 阶等差数列是递增数列,即公差
阶等差数列是递增数列,即公差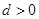 ,其和为0,故易知数列前面的项为负,后面的项为正,即前
,其和为0,故易知数列前面的项为负,后面的项为正,即前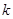 项为正,后
项为正,后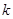 项为正,因此有
项为正,因此有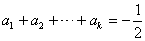 ,
,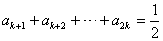 ,这两式用基本量或直接相减可求得
,这两式用基本量或直接相减可求得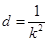 ,
,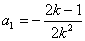 ,因此通项公式可得;(3)(i)我们只要把数列中所有非负数项的和记为
,因此通项公式可得;(3)(i)我们只要把数列中所有非负数项的和记为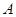 ,所有负数项的记为
,所有负数项的记为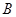 ,则
,则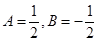 ,
,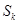 不可能比
不可能比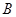 小,同样
小,同样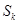 不可能比
不可能比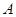 大,即
大,即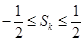 ,得证;(ii)若
,得证;(ii)若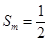 ,则一定有
,则一定有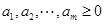 ,
,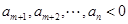 ,且
,且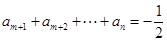 ,若数列
,若数列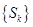 为n阶“期待数列”,设其前
为n阶“期待数列”,设其前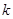 项和为
项和为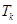 ,首先
,首先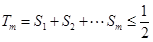 ,而
,而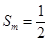 ,
,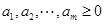 ,因此
,因此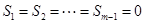 ,即
,即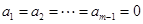 ,
,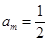 ,从而
,从而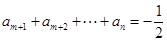 ,于是
,于是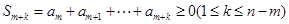 ,那么
,那么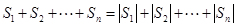 ,矛盾出现了,故结论是否定的.
,矛盾出现了,故结论是否定的.
试题解析:(1)①若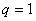 ,由①得,
,由①得,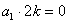 ,得
,得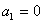 ,矛盾. 1分
,矛盾. 1分
若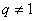 ,则由①
,则由①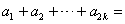
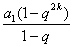 =0,得
=0,得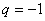 , 3分
, 3分
由②得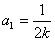 或
或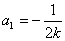 .
.
所以,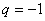 .数列
.数列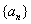 的通项公式是
的通项公式是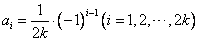
或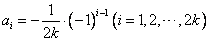 4分
4分
(2)设等差数列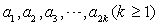 的公差为
的公差为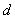 ,
,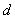 >0.
>0.
∵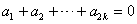 ,∴
,∴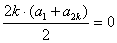 ,∴
,∴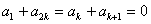 ,
,
∵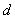 >0,由
>0,由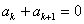 得
得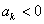 ,
,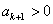 ,
,
由①、②得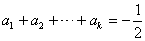 ,
,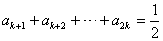 , 6分
, 6分
两式相减得,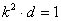 , ∴
, ∴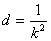 ,
,
又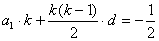 ,得
,得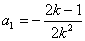 ,
,
∴数列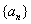 的通项公式是
的通项公式是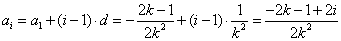 . 9分
. 9分
(3)记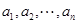 中所有非负项的和为A,所有负数项的和为B,
中所有非负项的和为A,所有负数项的和为B,
则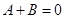 ,
,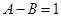 ,解得
,解得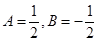 ,
,
(i)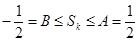 ,即
,即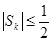 . 12分
. 12分
(ii)若存在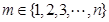 ,使
,使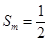 ,由前面的证明过程知:
,由前面的证明过程知:
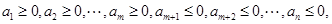
且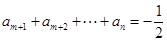 , 14分
, 14分
如果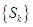 是
是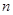 阶“期待数列”,
阶“期待数列”,
记数列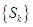
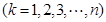 的前
的前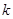 项和为
项和为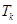 ,
,
则由(i)知,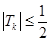 ,
,
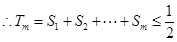 ,而
,而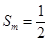 ,
,
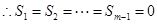 ,从而
,从而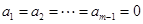 ,
,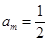 ,
,
又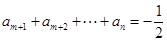 ,
,
则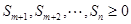 , 16分
, 16分
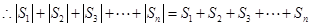 ,
,
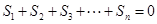 与
与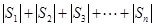
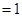 不能同时成立,
不能同时成立,
所以,对于有穷数列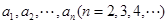 ,若存在
,若存在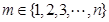 使
使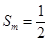 ,则数列
,则数列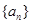 的和数列
的和数列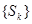
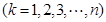 不能为
不能为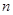 阶“期待数列”. 18分
阶“期待数列”. 18分
考点:(1)等比数列的前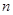 和公式与通项公式;(2)等差数列的前
和公式与通项公式;(2)等差数列的前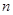 和公式与通项公式;(3)数列综合题.
和公式与通项公式;(3)数列综合题.


科目:高中数学 来源: 题型:
| y |
| x |
| x |
| y |
| x |
| x |
| x |
| 1 |
| 2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2014 |
| (2n-1)π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市徐汇区高三上学期期末考试(一模)文科数学试卷(解析版) 题型:解答题
称满足以下两个条件的有穷数列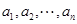 为
为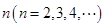 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若数列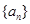 的通项公式是
的通项公式是 ,
,
试判断数列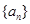 是否为2014阶“期待数列”,并说明理由;
是否为2014阶“期待数列”,并说明理由;
(2)若等比数列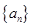 为
为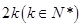 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及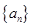 的通项公式;
的通项公式;
(3)若一个等差数列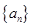 既是
既是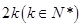 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com