
设点A和B为抛物线y2=4px(p>0)上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求点M的轨迹方程,并说明它表示什么曲线.
点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
点A、B在抛物线y2=4px上,
设A(![]() ,ya),B(
,ya),B(![]() ,yb),OA、OB的斜率分别为kOA、kOB,
,yb),OA、OB的斜率分别为kOA、kOB,
∴kOA=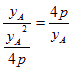 ,kOB=
,kOB=![]() .
.
由OA⊥OB,得kOA·kOB=![]() =-1. ①
=-1. ①
由点A在AB上,得直线AB的方程为
(ya+yb)(y-ya)=4p(x-![]() ). ②
). ②
由OM⊥AB,得直线OM方程为y=![]() x. ③
x. ③
设点M(x,y),则x、y满足②③两式,将②式两边同时乘以-![]() ,并利用③式
,并利用③式
整理得
![]() yA2+yyA-(x2+y2)=0. ④
yA2+yyA-(x2+y2)=0. ④
由③④两式得-![]() +yByA-(x2+y2)=0,
+yByA-(x2+y2)=0,
由①式知,yAyB=-16p2,
∴x2+y2-4px=0.
∵A、B是原点以外的两点,∴x≠0.
∴点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.


科目:高中数学 来源: 题型:
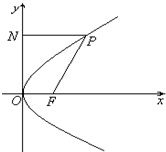 如图所示,点F(
如图所示,点F(| p |
| 2 |
| 1 |
| 2 |
| QA |
| QB |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
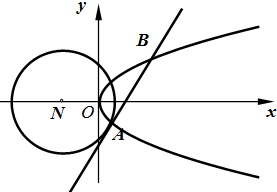 已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆的切线l与抛物线C交于不同的两点A,B,
已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆的切线l与抛物线C交于不同的两点A,B,| MA |
| MB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•烟台二模)已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
(2012•烟台二模)已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.| MA |
| MB |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练24练习卷(解析版) 题型:解答题
如图,已知抛物线C1:x2+by=b2经过椭圆C2: +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.

(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省宝鸡市高三教学质量检测(三)理科数学试卷(解析版) 题型:解答题
已知圆N:(x+2)2+y2=8和抛物线C: y2= 2x,圆N的切线l与抛物线C交于不同的两点A,B.
(I)当直线l的斜率为1时,求线段AB的长;
(II)设点M和点N关于直线y=x对称,问是否存在直线l,使得 ?若存在,求出直线l的方程;若不存在,请说明理由.
?若存在,求出直线l的方程;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com