
【题目】设集合 ![]() 存在正实数
存在正实数 ![]() ,使得定义域内任意
,使得定义域内任意 ![]() 都有
都有 ![]() .
.
(1)若 ![]() ,试判断
,试判断 ![]() 是否为
是否为 ![]() 中的元素,并说明理由;
中的元素,并说明理由;
(2)若 ![]() ,且
,且 ![]() ,求
,求 ![]() 的取值范围;
的取值范围;
(3)若 ![]() (
( ![]() ),且
),且 ![]() ,求
,求 ![]() 的最小值.
的最小值.
【答案】
(1)解:∵ ![]() , ∴
, ∴ ![]()
(2)解:由 ![]()
∴ ![]() ,
,
故 ![]()
(3)解:由 ![]() ,
,
即: ![]()
∴ ![]() 对任意
对任意 ![]() 都成立
都成立
∴ ![]()
当 ![]() 时,
时, ![]() ;
;
当 ![]() 时,
时, ![]() ;
;
当 ![]() 时,
时, ![]() .
.
综上: 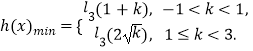
【解析】主要考查对函数定义域、值域及其最值的运用与计算。
【考点精析】利用函数的定义域及其求法和函数的值域对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤ ![]() )的部分图象如图所示,若方程f(x)=a在x∈[﹣
)的部分图象如图所示,若方程f(x)=a在x∈[﹣ ![]() ,
, ![]() ]上有两个不相等的实数根,则a的取值范围是( )
]上有两个不相等的实数根,则a的取值范围是( ) 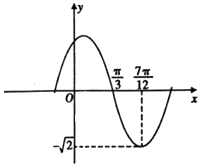
A.[ ![]() ,
, ![]() )
)
B.[﹣ ![]() ,
, ![]() )
)
C.[﹣ ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( ) 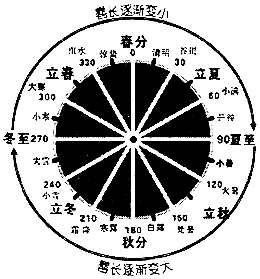
A.五寸
B.二尺五寸
C.三尺五寸
D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线E:x2=2py(p>0)焦点F且倾斜角的60°直线l与抛物线E交于点M,N,△OMN的面积为4.
(1)求抛物线E的方程;
(2)设P是直线y=﹣2上的一个动点,过P作抛物线E的切线,切点分别为A、B,直线AB与直线OP、y轴的交点分别为Q、R,点C、D是以R为圆心、RQ为半径的圆上任意两点,求∠CPD最大时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合 ![]() ,定义了一种运算“
,定义了一种运算“ ![]() ”,使得集合
”,使得集合 ![]() 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素 ![]() ,使得对任意
,使得对任意 ![]() ,都有
,都有 ![]() ,则称元素
,则称元素 ![]() 是集合
是集合 ![]() 对运算“
对运算“ ![]() ”的单位元素.例如:
”的单位元素.例如: ![]() ,运算“
,运算“ ![]() ”为普通乘法;存在
”为普通乘法;存在 ![]() ,使得对任意
,使得对任意 ![]() ,都有
,都有 ![]() ,所以元素
,所以元素 ![]() 是集合
是集合 ![]() 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“ ![]() ”:
”:
② ![]() ,运算“
,运算“ ![]() ”为普通减法;
”为普通减法;
② ![]() 表示
表示 ![]() 阶矩阵,
阶矩阵, ![]() },运算“
},运算“ ![]() ”为矩阵加法;
”为矩阵加法;
③ ![]() (其中
(其中 ![]() 是任意非空集合),运算“
是任意非空集合),运算“ ![]() ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“ ![]() ”有单位元素的集合序号为( )
”有单位元素的集合序号为( )
A.①②;
B.①③;
C.①②③;
D.②③.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表:
使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 ![]() =
= ![]() x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
A.8年
B.9年
C.10年
D.11年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的偶函数f(x),其导函数为f'(x),对任意x∈[0,+∞),均满足:xf'(x)>﹣2f(x).若g(x)=x2f(x),则不等式g(2x)<g(1﹣x)的解集是( )
A.(﹣∞,﹣1)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:方程x2+mx+1=0有两个不等的正实数根,命题q:方程4x2+4(m+2)x+1=0无实数根.若“p或q”为真命题,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com