
【题目】如图,椭圆![]() :
: ![]()
![]() 的焦距与椭圆
的焦距与椭圆![]() :
: ![]() 的短轴长相等,且
的短轴长相等,且![]() 与
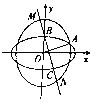
与![]() 的长轴长相等,这两个椭圆在第一象限的交点为
的长轴长相等,这两个椭圆在第一象限的交点为![]() ,直线
,直线![]() 经过
经过![]() 在
在![]() 轴正半轴上的顶点
轴正半轴上的顶点![]() 且与直线
且与直线![]() (
(![]() 为坐标原点)垂直,
为坐标原点)垂直, ![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,
, ![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求![]() 的标准方程;
的标准方程;
(2)求![]() .
.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右有顶点分别是
的左、右有顶点分别是![]() 、
、![]() ,上顶点是
,上顶点是![]() ,圆
,圆![]() :
:![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,且椭圆的右焦点与抛物线
,且椭圆的右焦点与抛物线![]() 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)平行于![]() 轴的动直线与椭圆和圆在第一象限内的交点分别为
轴的动直线与椭圆和圆在第一象限内的交点分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,![]() .试判断
.试判断![]() 是否为定值,若是,证明你的结论.若不是,举反例说明.
是否为定值,若是,证明你的结论.若不是,举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (限定
(限定![]() ).
).
(1)写出曲线![]() 的极坐标方程,并求
的极坐标方程,并求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)射线![]() 与曲线
与曲线![]() 与
与![]() 分别交于点
分别交于点![]() (
(![]() 异于原点),求
异于原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本
万元(总成本![]() 固定成本
固定成本![]() 生产成本).销售收入
生产成本).销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入
销售收入![]() 总成本);
总成本);
(2)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一次围棋比赛,每局胜者得1分,负者得0分,约定一方比另一方多3分或满9局时比赛结束,并规定:只有一方比另一方多三分才算赢,其它情况算平局,假设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
,各局比赛结果相互独立,已知前3局中,甲胜2局,乙胜1局.
(1) 求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 得分布列及数学期望.
得分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com