
【题目】如图,在三棱锥P﹣ABC中,E,F分别为AC,BC的中点.
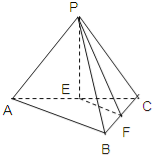
(1)求证:EF∥平面PAB;
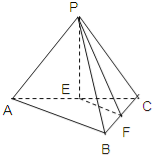
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求证:平面PEF⊥平面PBC.
【答案】见解析
【解析】
试题(1)利用E,F分别是AC,BC的中点,说明EF∥AB,通过直线与平面平行的判定定理直接证明EF∥平面PAB.
(2)证明PE⊥AC,利用平面与平面垂直的判定定理证明PE⊥平面ABC,通过证明PE⊥BC.EF⊥BC,EF∩PE=E,证明BC⊥平面PEF,然后推出平面PEF⊥平面PBC.
证明:(1)∵E,F分别是AC,BC的中点,∴EF∥AB.
又EF平面PAB,
AB平面PAB,
∴EF∥平面PAB.
(2)在三角形PAC中,∵PA=PC,E为AC中点,
∴PE⊥AC.
∵平面PAC⊥平面ABC,
平面PAC∩平面ABC=AC,
∴PE⊥平面ABC.
∴PE⊥BC.
又EF∥AB,∠ABC=90°,∴EF⊥BC,
又EF∩PE=E,
∴BC⊥平面PEF.
∴平面PEF⊥平面PBC.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
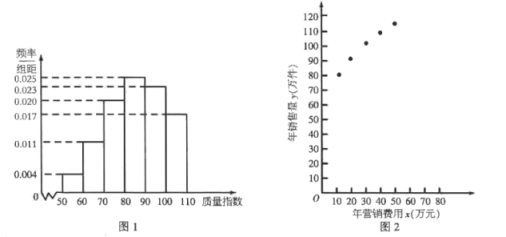
【题目】某公司生产一种产品,从流水线上随机抽取100件产品,统计其质量指数并绘制频率分布直方图(如图1):
产品的质量指数在![]() 的为三等品,在
的为三等品,在![]() 的为二等品,在
的为二等品,在![]() 的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
的为一等品,该产品的三、二、一等品的销售利润分别为每件1.5,3.5,5.5(单位:元),以这100件产品的质量指数位于各区间的频率代替产品的质量指数位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年的年营销费用
(单位:万件)的影响,对近5年的年营销费用![]() 和年销售量
和年销售量![]()
![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
16.30 | 24.87 | 0.41 | 1.64 |
表中![]() ,
,![]() ,
,![]() ,
,![]()
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
(ⅰ)建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(ⅱ)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?(收益=销售利润-营销费用,取![]() )
)
参考公式:对于一组数据:![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小乘估计分别为
的斜率和截距的最小乘估计分别为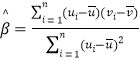 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥DABC中,ADDC,ACCB,AB=2AD=2DC=2,且平面ABD平面BCD,E为AC的中点.
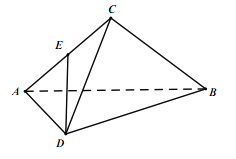
(I)证明:ADBC;
(II)求直线 DE 与平面ABD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,已知矩形ABCD满足AB=5,![]() ,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱
,沿平行于AD的线段EF向上翻折(点E在线段AB上运动,点F在线段CD上运动),得到如图②所示的三棱柱![]() .
.
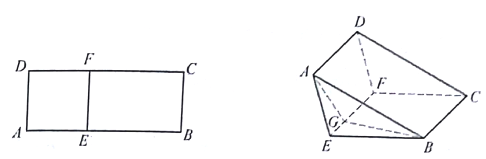
⑴若图②中△ABG是直角三角形,这里G是线段EF上的点,试求线段EG的长度x的取值范围;
⑵若⑴中EG的长度为取值范围内的最大整数,且线段AB的长度取得最小值,求二面角![]() 的值;
的值;
⑶在⑴与⑵的条件都满足的情况下,求三棱锥A-BFG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 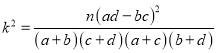 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了反映国民经济各行业对仓储物流业务的需求变化情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.如图所示的折线图是2016年1月至2017年12月的中国仓储指数走势情况.
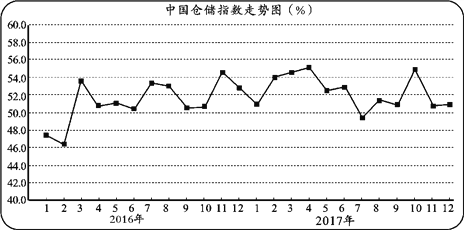
根据该折线图,下列结论正确的是
A. 2016年各月的仓储指数最大值是在3月份
B. 2017年1月至12月的仓储指数的中位数为54%
C. 2017年1月至4月的仓储指数比2016年同期波动性更大
D. 2017年11月的仓储指数较上月有所回落,显示出仓储业务活动仍然较为活跃,经济运行稳中向好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com