
【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c,1+ ![]() =
= ![]() .
.
(1)求A的大小;
(2)若△ABC为锐角三角形,求函数y=2sin2B﹣2cosBcosC的取值范围;
(3)现在给出下列三个条件:①a=1;②2c﹣( ![]() +1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
+1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
【答案】
(1)解:由题意得,1+ ![]() =
= ![]() ,
,
由正弦定理得,1+ ![]() =
= ![]() =
= ![]() ,
,
∴cosA= ![]() ,∴A=
,∴A= ![]() ;
;
(2)解:因为A+B+C=π,A= ![]() ,所以B+C=
,所以B+C= ![]() ,
,
则y=2sin2B﹣2cosBcosC=1﹣cos2B﹣2sinBcos( ![]() ﹣B)=
﹣B)= ![]() ﹣sin(2B+
﹣sin(2B+ ![]() )
)
又△ABC为锐角三角形,则 ![]() <B<
<B< ![]() ,∴
,∴ ![]() <2B+
<2B+ ![]() <
< ![]() ,所以sin(2B+
,所以sin(2B+ ![]() )∈(﹣
)∈(﹣ ![]() ,1),
,1),
所以y∈( ![]() ,2);
,2);
(3)解:方案一:选择①②,可确定△A BC,
因为A=60°,a=1,2c﹣( ![]() +1)b=0,
+1)b=0,
由余弦定理得: ![]() ,
,
整理得:b2= ![]() ,b=
,b= ![]() ,c=
,c= ![]() ,
,
所以S△ABC= ![]() =
= ![]()
方案二:选择①③,可确定△A BC,
因为 A=60°,B=45°,则C=75°,
由正弦定理b= ![]() =
= ![]() ,
,
所以S△ABC= ![]() =
= ![]() .
.
【解析】(1)根据切化弦、两角和的正弦公式和诱导公式化简已知的式子,由特殊角的三角函数值求出A;(2)由(1)和内角和定理表示出C,代入解析式利用二倍角公式,两角和与差和公式化简,根据锐角三角形列出不等式组求出B的范围,由正弦函数的性质求出函数的值域;(3)方案一:选择①②,由条件和余弦定理列出方程求出b的值,代入三角形的面积公式求解即可; 方案二:选择①③,由内角和定理和正弦定理分别求出C、c,入三角形的面积公式求解即可.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠PAC=30°,∠ACB=45°,BC=2 ![]() ,PA⊥AB.
,PA⊥AB. 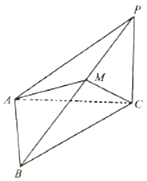
(1)求PC的长;
(2)若点M在侧棱PB上,且 ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形, ![]() ,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
(II)求二面角P﹣BC﹣D的余弦值.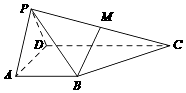
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥平面ABCD,BC⊥CD,PD=1,AB= ![]() ,BC=CD=
,BC=CD= ![]() ,AD=1.
,AD=1. 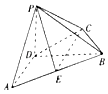
(1)求异面直线AB、PC所成角的余弦值;
(2)点E是线段AB的中点,求二面角E﹣PC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:y2=2px(p>0)与双曲线C2: ![]() =1(a>0.b>0)有公共焦点F,且在第一象限的交点为P(3,2
=1(a>0.b>0)有公共焦点F,且在第一象限的交点为P(3,2 ![]() ).
).
(1)求抛物线C1 , 双曲线C2的方程;
(2)过点F且互相垂直的两动直线被抛物线C1截得的弦分别为AB,CD,弦AB、CD的中点分别为G、H,探究直线GH是否过定点,若GH过定点,求出定点坐标;若直线GH不过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°、45°,且A、B两点之间的距离为60m,则树的高度为( ) 
A.(30+30 ![]() ) m
) m
B.(30+15 ![]() ) m??
) m??
C.(15+30 ![]() ) m
) m
D.(15+15 ![]() ) m
) m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心. 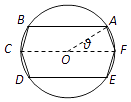
(1)把六边形ABCDEF的面积表示成关于θ的函数f(θ);
(2)当θ为何值时,可使得六边形区域面积达到最大?并求最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2+4ax+3a2<0,其中a≠0,命题q:实数x满足 ![]() .
.
(1)若a=﹣1,且p∨q为真,求实数x的取值范围;
(2)若¬p是¬q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com