
【题目】已知曲线![]() 在点
在点![]() 处的切线
处的切线![]() 平行直线
平行直线![]() ,且点
,且点![]() 在第三象限.
在第三象限.
(1)求![]() 的坐标;
的坐标;
(2)若直线![]() , 且
, 且![]() 也过切点
也过切点![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据曲线方程求出导函数,因为已知横线的斜率为![]() ,根据切线与已知直线平行得到斜率都为
,根据切线与已知直线平行得到斜率都为![]() ,所以令导函数等于
,所以令导函数等于![]() 得到关于
得到关于![]() 的方程,求出方程的接,即为切点的横坐标,代入曲线方程即可求解切点的纵坐标,又因为切点在第三象限,进而写出满足条件的切点坐标;(2)由直线
的方程,求出方程的接,即为切点的横坐标,代入曲线方程即可求解切点的纵坐标,又因为切点在第三象限,进而写出满足条件的切点坐标;(2)由直线![]() 的斜率为
的斜率为![]() ,根据两直线垂直时斜率乘积为
,根据两直线垂直时斜率乘积为![]() ,得出直线
,得出直线![]() 的斜率为
的斜率为![]() ,又根据(1)中求得切点坐标,写出直线
,又根据(1)中求得切点坐标,写出直线![]() 的方程即可.
的方程即可.
试题解析:⑴由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为 (-1,-4).
⑵∵直线![]() ,
,![]() 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为![]() ,
,
∵l过切点P0,点P0的坐标为 (-1,-4)
∴直线l的方程为![]() 即
即![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
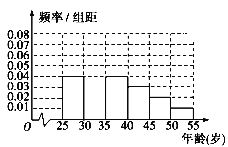
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[4,45)岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对函数”.现给出四个函数:
为“偏对函数”.现给出四个函数: 
![]() ;
; ![]() . 则其中是“偏对称函数”的函数个数为( )
. 则其中是“偏对称函数”的函数个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 。在以原点
。在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() 。
。
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知某曲线C的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求该曲线C的直角坐标系方程及离心率![]()
(2)已知点![]() 为曲线C上的动点,求点
为曲线C上的动点,求点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.(注:
垂直.(注: ![]() 为自然对数的底数)
为自然对数的底数)
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上存在极值,求实数
上存在极值,求实数![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com