
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4的四张卡片,现从甲、乙两个盒子中各取出一张卡片,每张卡片被取出的可能性相等.
(1)求取出的两张卡片上标号为相邻整数的概率;
(2)求取出的两张卡片上标号之和能被3整除的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先利用树状图法或列举法列出所有可能的结果,然后确定两张卡片上标号为相邻整数的所有可能结果的个数,利用古典概型的概率计算公式即可求解.
(2)利用树状图法或列举法列出所有可能的结果,然后确定两张卡片上标号之和能被3整除的所有可能结果的个数,利用古典概型的概率计算公式即可求解.
方法一 利用树状图列出从甲、乙两个盒子中各取出一张卡片的所有可能结果:
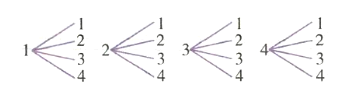
可以看出,试验的所有可能结果有16种.
(1)所取两张卡片上的标号为相邻整数的结果有1-2,2-1,2-3,3-2,3-4,4-3,共6种,故所求概率为![]() ,即取出的两张卡片上的标号为相邻整数的概率为
,即取出的两张卡片上的标号为相邻整数的概率为![]() .
.
(2)取出的两张卡片上的标号之和能被3整除的结果
有1-2,2-1,2-4,3-3,4-2,共5种,故所求概率为![]() ,即取出的两张卡片上的标号之和能被3整除的概率为
,即取出的两张卡片上的标号之和能被3整除的概率为![]() .
.
方法二 设从甲、乙两个盒子中各取一张卡片,其标号分别为![]() ,用
,用![]() 表示抽取结果,则所有可能的结果为
表示抽取结果,则所有可能的结果为![]() ,
,![]() ,
,![]() ,
,![]() ,共16种.
,共16种.
(1)所取两张卡片上的标号为相邻整数的结果有![]() ,共6种,故所求概率为
,共6种,故所求概率为![]() .
.
所以取出的两张卡片上的标号为相邻整数的概率为![]() .
.
(2)取出的两张卡片上的标号之和能被3整除的结果有![]() ,共5种,故所求概率为
,共5种,故所求概率为![]() ,所以取出的两张卡片上的标号之和能被3整除的概率为
,所以取出的两张卡片上的标号之和能被3整除的概率为![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】社会上有人认为在机动车驾驶技术上,男性优于女性,这是真的么?某社会调查机构与交警合作随机统计了经常开车的100名驾驶员最近三个月内是否有交通事故或交通违法事件发生,得到下面的列联表:
男 | 女 | 总计 | |
无 | 40 | 35 | 75 |
有 | 15 | 10 | 25 |
总计 | 55 | 45 | 100 |
附: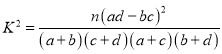
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
据此表,可得( ).
A.认为机动车驾驶技术与性别有关的可靠性不足![]()
B.认为机动车驾驶技术与性别有关的可靠性超过![]()
C.认为机动车驾驶技术与性别有关的可靠性超过![]()
D.认为机动车驾驶技术与性别有关的可靠性超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个由数字1,2,3,4,5,6,7,8,9组成的
是一个由数字1,2,3,4,5,6,7,8,9组成的![]() 位正整数,并同时满足如下两个条件:
位正整数,并同时满足如下两个条件:
(1)数字1,2,…,![]() 在
在![]() 中各出现两次;
中各出现两次;
(2)每两个相同的数字![]() 之间恰有
之间恰有![]() 个数字.
个数字.
此时,我们称这样的正整数![]() 为“好数”.例如,当
为“好数”.例如,当![]() 时,
时,![]() 可以是312 132.试确定满足条件的正整数
可以是312 132.试确定满足条件的正整数![]() 的值,并各写出一个相应的好数
的值,并各写出一个相应的好数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品;当
时,产品为二等品;当![]() 时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
时,产品为三等品.现有甲、乙两条生产线,各生产了100件该产品,测量每件产品的质量指标值,得到下面的试验结果.(以下均视频率为概率)
甲生产线生产的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
乙生产线产生的产品的质量指标值的频数分布表:
指标值分组 |
|
|
|
|
|
频数 | 10 | 15 | 25 | 30 | 20 |
(1)若从乙生产线生产的产品中有放回地随机抽取3件,求至少抽到2件三等品的概率;
(2)若该产品的利润率![]() 与质量指标值
与质量指标值![]() 满足关系:
满足关系: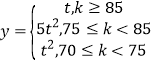 ,其中
,其中![]() ,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
,从长期来看,哪条生产线生产的产品的平均利润率更高?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为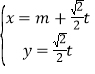 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com