练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知双曲线的中心在原点,焦点在坐标轴上，离心率为，且过点.

    （1）求双曲线的方程；

    （2）若点在双曲线上，求 的面积.

    【答案】（1）；(2).

    【解析】

    （1）设出双曲线的方程，代入点P的坐标，即可得到双曲线的方程；

    （2）利用点M（3，m）在双曲线上，求出m值，进而利用S|F1F2||m|，即可求△F1MF2的面积．

    解：（1）∵，∴可设双曲线的方程x2﹣y2＝λ

    ∵双曲线过点P（4，），∴16﹣10＝λ，即λ＝6

    ∴双曲线的方程x2﹣y2＝6

    （2）由（1）知，双曲线中a＝b

    ∴，∴，

    ∴|F1F2|＝4

    ∵点M（3，m）在双曲线上，∴9﹣m2＝6，∴|m|

    ∴△F1MF2的面积为S|F1F2||m|＝6

    即△F1MF2的面积为6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是中国古代数学专著，其中的“更相减损术”可以用来求两个数的最大公约数，即“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之.”翻译成现代语言如下：第一步，任意给定两个正整数，判断它们是否都是偶数，若是，用2约简；若不是，执行第二步：第二步，以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数，继续这个操作，知道所得的数相等为止，则这个数（等数）或这个数与约简的数的乘积就是所求的最大公约数.现给出更相减损术的程序图如图所示，如果输入的，，则输出的为（ ）.

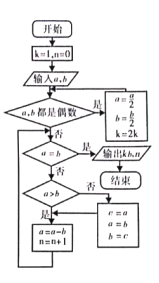
    A. 3B. 6C. 7D. 8

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，当P(x，y)不是原点时，定义P的“伴随点”为；

    当P是原点时，定义P的“伴随点“为它自身，平面曲线C上所有点的“伴随点”所构成的曲线定义为曲线C的“伴随曲线”.现有下列命题：

    ①若点A的“伴随点”是点，则点的“伴随点”是点A

    ②单位圆的“伴随曲线”是它自身；

    ③若曲线C关于x轴对称，则其“伴随曲线”关于y轴对称；

    ④一条直线的“伴随曲线”是一条直线.

    其中的真命题是_____________（写出所有真命题的序列）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的短轴长为，离心率为，过右焦点的直线与椭圆交于不同两点，.线段的垂直平分线交轴于点.

    （1）求椭圆的方程；

    （2）求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点P是抛物线上一动点，则点P到点的距离与P到直线的距离和的最小值是（ ）

    A.B.C.3D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为（,a为常数）），过点、倾斜角为的直线的参数方程满足，（为参数）．

    （1）求曲线C的普通方程和直线的参数方程；

    （2）若直线与曲线C相交于A、B两点（点P在A、B之间），且，求和的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在梯形ABCD中,AD//BC,∠ABC=，,∠ADC=，PA⊥平面ABCD且PA=.

    (1)求直线AD到平面PBC的距离；

    (2)求出点A到直线PC的距离；

    (3)在线段AD上是否存在一点F,使点A到平面PCF的距离为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线 的两条渐近线与抛物线的准线分别交于，两点．若双曲线的离心率为，的面积为，为坐标原点，则抛物线的焦点坐标为 ( )

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的左、右焦点分别为点，，其离心率为，短轴长为.

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）过点的直线与椭圆交于，两点，过点的直线与椭圆交于，两点，且，证明：四边形不可能是菱形.

    查看答案和解析>>

    同步练习册答案