Question

函数f(x)的定义域为D={x|x≠0},且满足对于任意x₁、x₂∈D,有f(x₁·x₂)=f(x₁)+f(x₂).

(1)求f(1)的值；

(2)判断f(x)的奇偶性并证明；

(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函数，求x的取值范围.

Answer 1

(1)解:令x₁=x₂=1,有f(1×1)=f(1)+f(1),解得f(1)=0.

(2)证明:令x₁=x₂=-1,有f［(-1)×(-1)］=f(-1)+f(-1).解得f(-1)=0.

    令x₁=-1,x₂=x,有f(-x)=f(-1)+f(x),∴f(-x)=f(x).

    ∴f(x)为偶函数.

(3)解:f(4×4)=f(4)+f(4)=2,f(16×4)=f(16)+f(4)=3.

    ∴f(3x+1)+f(2x-6)≤3,即f［(3x+1)(2x-6)］≤f(64).               (*)

    ∵f(x)在(0,+∞)上是增函数，

    ∴(*)等价于不等式组

   

    或

    即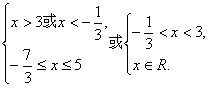

    ∴3＜x≤5或-≤x＜-或-＜x＜3.?

    ∴x的取值范围为{x|-≤x＜-或-＜x＜3或3＜x≤5}.

讲评:解答本题易出现如下思维障碍:

    (1)无从下手，不知如何脱掉“f”.解决办法:利用函数的单调性.

    (2）无法得到另一个不等式.解决办法:关于原点对称的两个区间上，奇函数的单调性相同，偶函数的单调性相反.