
 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 上的单调性.
上的单调性.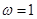 (2)
(2)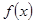 在
在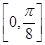 单调递增,在
单调递增,在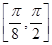 单调递减.
单调递减.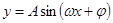 的形式,利用公式
的形式,利用公式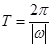 计算周期.(2)利用正弦函数的单调区间,求在
计算周期.(2)利用正弦函数的单调区间,求在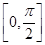 的单调性.(3)求三角函数的最小正周期一般化成
的单调性.(3)求三角函数的最小正周期一般化成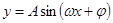 ,
,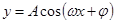 ,
,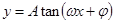 形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成
形式,利用周期公式即可.(4)求解较复杂三角函数的单调区间时,首先化成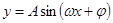 形式,再
形式,再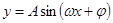 的单调区间,只需把
的单调区间,只需把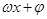 看作一个整体代入
看作一个整体代入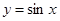 相应的单调区间,注意先把
相应的单调区间,注意先把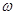 化为正数,这是容易出错的地方.
化为正数,这是容易出错的地方.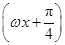
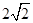 sin ωx·cos ωx+
sin ωx·cos ωx+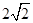 cos2ωx
cos2ωx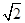 (sin 2ωx+cos 2ωx)+
(sin 2ωx+cos 2ωx)+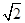
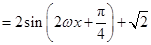 3分
3分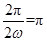 ,故ω=1. 6分
,故ω=1. 6分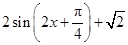 .
.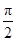 ,则
,则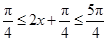 .
.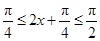 ,即
,即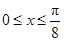 时,f(x)单调递增;
时,f(x)单调递增;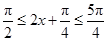 ,即
,即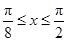 时,f(x)单调递减. 10分
时,f(x)单调递减. 10分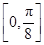 上单调递增,在区间
上单调递增,在区间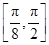 上单调递减. 12分
上单调递减. 12分

科目:高中数学 来源:不详 题型:单选题
| A.sin(B+C)=sinA | B.cos(B+C)=cosA |
| C.tan(B+C)=tanA | D.cot(B+C)=cotA |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
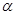 ,使
,使
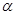 ,使
,使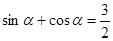
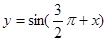 是偶函数
是偶函数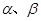 是第一象限的角,且
是第一象限的角,且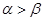 ,则
,则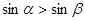 .其中正确命题的序号是________________.
.其中正确命题的序号是________________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com