
分析 (Ⅰ)由直线的斜率公式整理即可求得曲线E轨迹的方程;
(Ⅱ)由题意可知:设其直线方程为:x=my-1,代入直线方程,由韦达定理及向量的数量积的坐标运算,则$\overrightarrow{AC}$•$\overrightarrow{AD}$=0,即可求得AC⊥AD;
(Ⅲ)即SACOD=2S△COD,SACOD=2×$\frac{1}{2}$丨OQ丨丨y1-y2丨,由(Ⅱ)即可求得SACOD═2$\sqrt{-\frac{3}{({m}^{2}+3)^{2}}+\frac{4}{{m}^{2}+3}}$,即可求得四边形ACOD面积的最大值.
解答 解:(Ⅰ)由题意可知:$\frac{y}{x-2}$•$\frac{y}{x+2}$=-$\frac{1}{3}$(x≠2),整理得:$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$(x≠2),
曲线E的方程:$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$(x≠2);
(Ⅱ)当直线CD的斜率不为0时,过点Q(-1,0),设其直线方程为:x=my-1,C(x1,y1),D(x2,y2),
则$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1}\\{x=my-1}\end{array}\right.$,:整理得:(m2+3)y2-2my-3=0,
则y1+y2=$\frac{2m}{{m}^{2}+3}$,y1y2=-$\frac{3}{{m}^{2}+3}$.
$\overrightarrow{AC}$=(x1+2,y1),$\overrightarrow{AD}$=(x2+2,y2),
∴$\overrightarrow{AC}$•$\overrightarrow{AD}$=(x1+2,y1)•(x2+2,y2),
=(m2+1)y1y2+m(y1+y2)+1,
=(m2+1)(-$\frac{3}{{m}^{2}+3}$)+m•$\frac{2m}{{m}^{2}+3}$+1,
=$\frac{-3({m}^{2}+1)+2{m}^{2}+{m}^{2}+3}{{m}^{2}+3}$=0,
∴AC⊥AD.
(Ⅲ)由Q是A,O中点,则四边形ACOD的面积为2倍的三角形COD的面积,即SACOD=2S△COD,
SACOD=2×$\frac{1}{2}$丨OQ丨丨y1-y2丨=$\sqrt{({y}_{1}-{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(\frac{2m}{{m}^{2}+3})^{2}+\frac{12}{{m}^{2}+3}}$,
=2$\sqrt{\frac{4{m}^{2}+9}{({m}^{2}+3)^{2}}}$,
=2$\sqrt{-\frac{3}{({m}^{2}+3)^{2}}+\frac{4}{{m}^{2}+3}}$,
当m=0时,四边形ACOD面积最大,最大值为2.
点评 本题考查轨迹方程,考查直线与椭圆的位置关系,考查韦达定理及弦长公式的应用,考查向量数量积的坐标运算及三角形面积公式的综合应用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | $3+3\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 《雷雨》只能在周二上演 | B. | 《茶馆》可能在周二或周四上演 | ||
| C. | 周三可能上演《雷雨》或《马蹄声碎》 | D. | 四部话剧都有可能在周二上演 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
教育模式 人数(人) | 在线测评 | 在线课堂 | 自主学习 | 线下延伸 |
| 25 | √ | √ | √ | |
| 45 | √ | |||
| 40 | √ | √ | ||
| 30 | √ | √ | √ | |
| 40 | √ | √ | ||
| 20 | √ | √ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
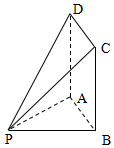 如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{\sqrt{2016}}}$ | B. | $\frac{1}{{\sqrt{2017}}}$ | C. | $\frac{1}{{\sqrt{2018}}}$ | D. | $\frac{1}{{\sqrt{2019}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com