
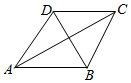
 如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).
如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).分析 (1)根据向量数量积的公式进行计算即可,
(2)根据三角形的面积公式,结合三角函数辅助角公式进行化简,结合三角形的图象和性质进行求解即可.
(3)根据三角形的面积公式,结合三角函数辅助角公式进行化简,结合三角形的图象和性质进行求解即可.
解答 解:(1)设AC∩BD=0,则O是BD的中点,且AC⊥BD,
当α=$\frac{π}{2}$时,AO=$\sqrt{2}$,OC=$\sqrt{6}$,
则$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\overrightarrow{AC}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AC}$2-$\overrightarrow{AC}$•$\overrightarrow{AB}$=($\sqrt{2}+\sqrt{6}$)2-($\sqrt{2}+\sqrt{6}$)•$\sqrt{2}$=2$\sqrt{3}$+6.
(2)由题意得BC=BD=4sin$\frac{α}{2}$,
则S=$\frac{1}{2}$AB•BCsin∠ABC=$\frac{1}{2}×2×4$sin$\frac{α}{2}$•sin($\frac{π}{6}$+$\frac{α}{2}$)=4sin$\frac{α}{2}$•sin($\frac{π}{6}$+$\frac{α}{2}$)=4sin$\frac{α}{2}$•(sin$\frac{π}{6}$cos$\frac{α}{2}$+cos$\frac{π}{6}$sin$\frac{α}{2}$)=4sin$\frac{α}{2}$•($\frac{1}{2}$cos$\frac{α}{2}$+$\frac{\sqrt{3}}{2}$sin$\frac{α}{2}$)
=2sin$\frac{α}{2}$cos$\frac{α}{2}$+2$\sqrt{3}$sin2$\frac{α}{2}$=sinα+$\sqrt{3}$(1-cosα)=2sin(α-$\frac{π}{3}$)+$\sqrt{3}$,
∵0<α<π,∴-$\frac{π}{3}$<α-$\frac{π}{3}$<$\frac{2π}{3}$,
∴当α-$\frac{π}{3}$=$\frac{π}{2}$,即α=$\frac{5π}{6}$时,S取得最大值,此时S=2+$\sqrt{3}$.
(3)由题意得BC=BD=4sin$\frac{α}{2}$,
S=f(α)=$\frac{\sqrt{3}}{4}$(4sin$\frac{α}{2}$)2=4$\sqrt{3}$•$\frac{1-cosα}{2}$=-2$\sqrt{3}$cosα+2$\sqrt{3}$,
则g(α)=-2$\sqrt{3}$cosα+2$\sqrt{3}$-2sinα=-4sin(α+$\frac{π}{3}$)+2$\sqrt{3}$,
∵0<α<π,∴$\frac{π}{3}$<α+$\frac{π}{3}$<$\frac{4π}{3}$,
∴当α+$\frac{π}{3}$=$\frac{π}{2}$,即α=$\frac{π}{6}$时,g(α)取得最小值,
故g(α)=f(α)-2sinα的最小值为g($\frac{π}{6}$)=2$\sqrt{3}$-4.
点评 本题主要考查向量数量积与三角函数的综合应用,根据向量数量积的公式以及辅助角公式进行化简是解决本题的关键.考查学生的运算能力.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{63}$ | B. | $\frac{1}{31}$ | C. | $\frac{3}{61}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{ED}$ | C. | $\overrightarrow{BE}$ | D. | $\overrightarrow{BC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com