
【题目】![]() 年
年![]() 月
月![]() 日,小刘从各个渠道融资
日,小刘从各个渠道融资![]() 万元,在某大学投资一个咖啡店,
万元,在某大学投资一个咖啡店,![]() 年
年![]() 月
月![]() 日正式开业,已知开业第一年运营成本为
日正式开业,已知开业第一年运营成本为![]() 万元,由于工人工资不断增加及设备维修等,以后每年成本增加
万元,由于工人工资不断增加及设备维修等,以后每年成本增加![]() 万元,若每年的销售额为
万元,若每年的销售额为![]() 万元,用数列
万元,用数列![]() 表示前
表示前![]() 年的纯收入.(注:纯收入
年的纯收入.(注:纯收入![]() 前
前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额)
投资额)
(1)试求年平均利润最大时的年份(年份取正整数)并求出最大值.
(2)若前![]() 年的收入达到最大值时,小刘计划用前
年的收入达到最大值时,小刘计划用前![]() 年总收入的
年总收入的![]() 对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
对咖啡店进行重新装修,请问:小刘最早从哪一年对咖啡店进行重新装修(年份取整数)?并求小刘计划装修的费用.
【答案】(1)到![]() 年或
年或![]() 年,年平均利润最大,最大值为
年,年平均利润最大,最大值为![]() 万元;(2)小刘最早从
万元;(2)小刘最早从![]() 年对咖啡店进行重新装修,计划装修费用为
年对咖啡店进行重新装修,计划装修费用为![]() 万元.
万元.
【解析】
(1)每年的运营成本构成一个等差数列,每年的销售额是一个常数列,根据题意,列出等式年平均利润为![]() ,之后应用基本不等式,结合
,之后应用基本不等式,结合![]() 求得结果;
求得结果;
(2)由(1)知![]() ,利用二次函数的性质以及
,利用二次函数的性质以及![]() 的条件,得到当
的条件,得到当![]() 或
或![]() 时,
时,![]() 取得最大值
取得最大值![]() ,进而得到结果.
,进而得到结果.
(1)由条件可知,每年的运营成本构成首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
![]() ,
,
则年平均利润为![]() ,
,
由![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
但![]() ,且
,且![]() 或
或![]() 时,
时,![]() .
.
此时,![]() 取最大值
取最大值![]() .
.
![]() 到
到![]() 年或
年或![]() 年,年平均利润最大,最大值为
年,年平均利润最大,最大值为![]() 万元;
万元;
(2)由(1)可得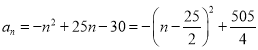
![]() ,
,
当![]() 或
或![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
![]() (万元)
(万元)
故小刘最早从![]() 年对咖啡店进行重新装修,计划装修费用为
年对咖啡店进行重新装修,计划装修费用为![]() 万元.
万元.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】高二全体师生今秋开学前在新校区体验周活动中有优异的表现,学校拟对高二年级进行表彰;
(1)若要表彰3个优秀班级,规定从6个文科班中选一个,14个理科班中选两个班级,有多少种不同的选法?
(2)年级组拟在选出的三个班级中再选5名学生,每班至少1名,最多2名,则不同的分配方案有多少种?
(3)选中的这5名学生和三位年级负责人徐主任,陈主任,付主任排成一排合影留念,规定这3位老师不排两端,且老师顺序固定不变,那么不同的站法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
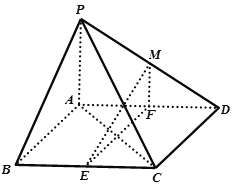
(1)若![]() 为
为![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,曲线C的参数方程是
轴的正半轴,建立平面直角坐标系,曲线C的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 被曲线C截得的弦长;
被曲线C截得的弦长;
(2)从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次田径比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。

若将运动员按成绩由好到差编为1—35号,再用系统抽样方法从中抽取5人,则其中成绩在区间![]() 上的运动员人数为
上的运动员人数为
A.6B.5C.4D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com