解:(1)由f(x)=x+

,得
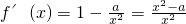
,
当a<0时,
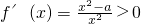
恒成立,所以函数y=f(x)在(0,+∞)上为增函数;
当a>0时,令
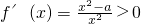
,解得
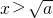
,令
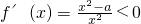
,解得
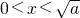
,
所以函数y=f(x)在
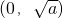
上为减函数;在
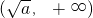
上为增函数.
(2)由(1)可知当a<0时,函数y=f(x)在(0,+∞)上为增函数,此时函数的值域为R,不合题意;
当a>0时,函数y=f(x)在
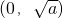
上为减函数;在
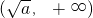
上为增函数,
此时函数的值域为
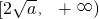
,即
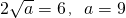
.
综上,a=9.
分析:(1)由函数的解析式f(x)求出导函数,然后分a小于0和a大于0两种情况,分别令导函数大于0列出关于a的不等式,求出不等式的解集即可得到a的取值范围即为函数的递增区间;令导函数小于0列出关于a的不等式,求出不等式的解集即可得到a的范围即为函数的递减区间;(2)由(1)知,当a小于0时,函数在区间(0,+∞)上单调递增,值域为R,不合题意;当a大于0时,根据函数的增减性得到函数的最小值为f(

),求出f(

)的值即可得到函数的值域,又函数的值域为[6,+∞),所以得到f(

)的值等于6,列出关于a的方程,求出方程的解即可得到a的值.
点评:此题考查学生会利用导函数的正负得到函数的单调区间,会根据函数的增减性得到函数的最值,掌握导数在最值问题中的应用,是一道综合题.

 (x>0),a为常数,且a≠0.
(x>0),a为常数,且a≠0. ,得
,得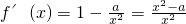 ,
,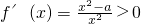 恒成立,所以函数y=f(x)在(0,+∞)上为增函数;
恒成立,所以函数y=f(x)在(0,+∞)上为增函数;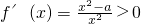 ,解得
,解得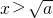 ,令
,令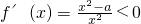 ,解得
,解得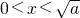 ,
,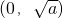 上为减函数;在
上为减函数;在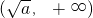 上为增函数.
上为增函数.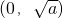 上为减函数;在
上为减函数;在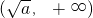 上为增函数,
上为增函数,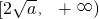 ,即
,即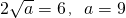 .
. ),求出f(
),求出f( )的值即可得到函数的值域,又函数的值域为[6,+∞),所以得到f(
)的值即可得到函数的值域,又函数的值域为[6,+∞),所以得到f( )的值等于6,列出关于a的方程,求出方程的解即可得到a的值.
)的值等于6,列出关于a的方程,求出方程的解即可得到a的值.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<