若存在实数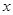
满足不等式
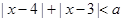，则实数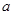
的取值范围是( )
A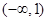． | B． |
C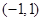． | D． |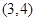
B
解析试题分析：解：设f（x）=|x-4|+|x-3|，当x＜3时，f（x）=-（x-4）-（x-3）=-2x+7，
故此时有f（x）=-2x+7＞1．，当x＞4，f（x）=（x-4）+（x-3）=2x-7，，故此时有f（x）=2x-7＞1．，当3≤x≤4，f（x）=-（x-4）+（x-3）=1，，综上所述f（x）的最小值为1，，又因为原不等式|x-4|+|x-3|＜a有实数解，只要a大于f（x）的最小值即可．，所以a的取值范围是（1，+∞）．故选B.
考点：绝对值不等式的解法
点评：此题主要考查绝对值不等式的解法，对于含有一个绝对值的不等式可以直接去绝对值号求解，对于含有两个绝对值号的绝对值不等式需要用分类讨论的方法去绝对值号．同学们需要注意选择合适的解法
名校课堂系列答案科目：高中数学 来源： 题型：单选题
若定义在R上的函数f(x)满足
,且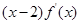
<0，a="f" (
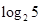),b="f" (
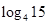),c="f" (
)，则a,b,c的大小关系为
| A．a>b>c | B．c>b>a | C．b>a>c | D．c>a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则不等式
的解集为 （ ）
和不等式
的解集相同，则
的值为（ ）
，
，对于任意
，不等式
恒成立，则实数
的取值范围为（ ）
>0的解集为(-1，2)，
是
和
的等比中项，那么
=
的解集是
,
,则
满足（ ）
