
分析 根据题意,设A(x1,y1)、B(x2,y2),求出经过点A、点B的圆的切线分别为x1x+y1y=r2、x2x+y2y=r2.而点P是这两条直线的公共点,代入直线方程并利用比较系数法,可得所求直线AB的方程.
解答 证明:设A(x1,y1)、B(x2,y2),
则设P(x,y)为过A的切线上一点,可得$\overrightarrow{AP}$=(x-x1,y-y1)
∵$\overrightarrow{AP}•\overrightarrow{OA}$=0,得x1(x-x1)+y1(y-y1)=0,化简得x1x+y1y=x12+y12
∵点A在圆x2+y2=r2上,可得x12+y12=r2
∴经过点A的圆的切线为x1x+y1y=r2,
同理可得经过点B的圆的切线为x2x+y2y=r2.
又∵点P(a,b)是两切线的交点,
∴可得ax1+by1=r2,说明点A(x1,y1)在直线ax+by=r2上;
同理ax2+by2=r2,说明点B(x2,y2)在直线ax+by=r2上
因此可得直线AB方程为:ax+by=r2.
点评 本题求圆的切点弦所在直线方程,解题量请注意与所学过圆上一点的切线的联系,体现由不熟悉向熟悉的转化,并注意直线方程形的特点,属于中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:解答题
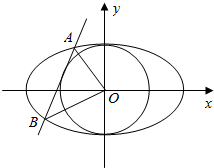 如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B.
如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com