
| y |
| x |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 2 |
| 2y2 |
| 3 |
| x2 |
| 2-k |
| y2 |
| 3-k |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| (a+1)2 |
| 2 |
| 5 |
| y |
| x |
| c |
| a |
| y |
| x |
| y-0 |
| x-0 |
| y |
| x |
| |2k| | ||
|
| 3 |
| 3 |
| y |
| x |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 2 |
| x2 |
| 2 |
| 2y2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| x2 |
| 2-k |
| y2 |
| 3-k |
| 2 | ||
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| (a+1)2 |
| c2 |
| a2 |
| a2+(a+1)2 |
| a2 |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| 5 |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| Іа |
| 3 |
| 5Іа |
| 12 |
| Іа |
| 2 |
| Іа |
| 4 |
| Іа |
| 4 |
| Іа |
| 4 |
| Іа |
| 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЕЅбЁЬт
 ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ ЃЛЂкЭждВ
ЃЛЂкЭждВ гыЭждВ
гыЭждВ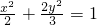 гаЯрЭЌЕФРыаФТЪЃЛЂлЫЋЧњЯп
гаЯрЭЌЕФРыаФТЪЃЛЂлЫЋЧњЯп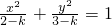 ЕФНЙЕузјБъЪЧЃЈ1ЃЌ0ЃЉЃЌЃЈ-1ЃЌ0ЃЉЂмдВx2+y2=1гыжБЯпy=kx+2УЛга ЙЋЙВЕуЕФГфвЊЬѕМўЪЧ
ЕФНЙЕузјБъЪЧЃЈ1ЃЌ0ЃЉЃЌЃЈ-1ЃЌ0ЃЉЂмдВx2+y2=1гыжБЯпy=kx+2УЛга ЙЋЙВЕуЕФГфвЊЬѕМўЪЧ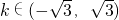 ЂнЩшaЃО1ЃЌдђЫЋЧњЯп
ЂнЩшaЃО1ЃЌдђЫЋЧњЯп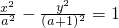 ЕФРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ
ЕФРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ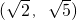 ЃЎ
ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКВЛЯъ ЬтаЭЃКЕЅбЁЬт
| y |
| x |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 2 |
| 2y2 |
| 3 |
| x2 |
| 2-k |
| y2 |
| 3-k |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| (a+1)2 |
| 2 |
| 5 |
| AЃЎЂйЂкЂл | BЃЎЂкЂлЂм | CЃЎЂйЂкЂлЂн | DЃЎЂйЂкЂмЂн |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2009-2010бЇФъББОЉДѓбЇИНжаИпШ§ЃЈЩЯЃЉЪ§бЇСЗЯАЪдОэ9ЃЈРэПЦЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
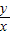 ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ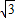 ЃЛЂкЭждВ
ЃЛЂкЭждВ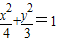 гыЭждВ
гыЭждВ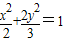 гаЯрЭЌЕФРыаФТЪЃЛЂлЫЋЧњЯп
гаЯрЭЌЕФРыаФТЪЃЛЂлЫЋЧњЯп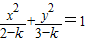 ЕФНЙЕузјБъЪЧЃЈ1ЃЌ0ЃЉЃЌЃЈ-1ЃЌ0ЃЉЂмдВx2+y2=1гыжБЯпy=kx+2УЛга ЙЋЙВЕуЕФГфвЊЬѕМўЪЧ
ЕФНЙЕузјБъЪЧЃЈ1ЃЌ0ЃЉЃЌЃЈ-1ЃЌ0ЃЉЂмдВx2+y2=1гыжБЯпy=kx+2УЛга ЙЋЙВЕуЕФГфвЊЬѕМўЪЧ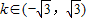 ЂнЩшaЃО1ЃЌдђЫЋЧњЯп
ЂнЩшaЃО1ЃЌдђЫЋЧњЯп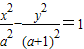 ЕФРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ
ЕФРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ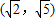 ЃЎ
ЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com