(Ⅰ)解:函数的定义域为(0,+∞),求导数
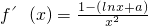
,
令f′(x)=0得x=e
1-a,
当x∈(0,e
1-a)时,f′(x)>0,∴f(x)是增函数;
当x∈(e
1-a,+∞),f′(x)<0,∴f(x)是减函数;
∴f(x)在x=e
1-a处取得极大值,f(x)
极大值=f(e
1-a)=e
a-1,无极小值.
(Ⅱ)解:①当e
1-a<e
2,即a>-1时,
由(Ⅰ)知,f(x)在(0,e
1-a)上是增函数,在(e
1-a,e
2)上是减函数,
∴
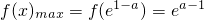
…(7分)
∵若函数f(x)的图象与函数g(x)=1的图象在区间(0,e
2]上有公共点,
∴e
a-1≥1
∴a≥1
∵a>-1,∴a≥1
②当e
1-a≥e
2,即a≤-1时,f(x)在区间(0,e
2]上是增函数,
∴f(x)在区间(0,e
2]上的最大值为f(e
2)=

∴原问题等价于

∴a≥e
2-2
∵a≤-1,∴无解
综上,实数a的取值范围是[1,+∞).
(Ⅲ)证明:令a=1,由(Ⅰ)知,
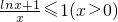
,∴lnx≤x-1,
∵a
1=1,假设

,则a
k+1=lna
k+a
k+2>1,故
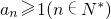
从而a
n+1=lna
n+a
n+2≤2a
n+1
∴
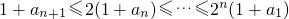
即
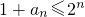
,
∴

.
分析:(Ⅰ)确定函数的定义域,求导数,确定函数的单调性,从而可得函数的极值;
(Ⅱ)分类讨论:①当e
1-a<e
2,即a>-1时,f(x)在(0,e
1-a)上是增函数,在(e
1-a,e
2)上是减函数,可得函数的最值,利用函数f(x)的图象与函数g(x)=1的图象在区间(0,e
2]上有公共点,可得实数a的取值范围;
②当e
1-a≥e
2,即a≤-1时,f(x)在区间(0,e
2]上是增函数,可得函数的最值,利用函数f(x)的图象与函数g(x)=1的图象在区间(0,e
2]上有公共点,从而可得结论;
(Ⅲ)先证明lnx≤x-1,从而可证a
n+1=lna
n+a
n+2≤2a
n+1,由此可证结论.
点评:本题考查导数知识的运用,考查函数而得单调性与极值,考查分类讨论的数学思想,考查不等式的证明,属于中档题.

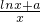 (a∈R)
(a∈R)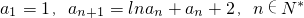 ,求证:
,求证: .
.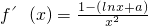 ,
,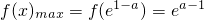 …(7分)
…(7分)

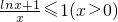 ,∴lnx≤x-1,
,∴lnx≤x-1, ,则ak+1=lnak+ak+2>1,故
,则ak+1=lnak+ak+2>1,故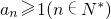
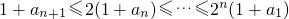
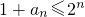 ,
, .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案