
【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() .
.
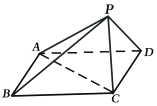
(1)证明:面![]() ⊥面
⊥面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)要证面面垂直,一般先证线面垂直,设AC与BD交点为O,则PO⊥BD,而正方形中AC⊥BD,于是可证得结论.
(2)由线面角的定义可得![]() ,以A为坐标原点,
,以A为坐标原点,![]() 为x,y轴的正方向建立空间直角坐标系,然后写出各点坐标,求出面BPC和面DPC的法向量,再由法向量的夹角的余弦值得二面角的余弦.
为x,y轴的正方向建立空间直角坐标系,然后写出各点坐标,求出面BPC和面DPC的法向量,再由法向量的夹角的余弦值得二面角的余弦.
(1)证明:连接AC,BD交点为O,∵四边形ABCD为正方形,∴![]()
∵![]() ,
,![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]()
又![]() ,∴
,∴![]() .
.
(2)∵![]() ,过点P做
,过点P做![]() ,垂足为E
,垂足为E
∴![]() ∵PA与底面ABCD所成的角为
∵PA与底面ABCD所成的角为![]() ,∴
,∴![]() ,
,
又![]() ,设
,设![]() ,则
,则
![]()
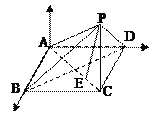
如图所示,以A为坐标原点,![]() 为x,y轴的正方向建立空间直角坐标系
为x,y轴的正方向建立空间直角坐标系![]()
![]()
设面![]() 法向量为
法向量为![]() ,
,![]()
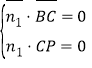 ,∴
,∴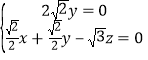 ,
,
![]() ,∴
,∴![]()
同理![]() 的法向量
的法向量![]() ,
,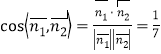
∴求二面角![]() 的余弦值
的余弦值![]()


科目:高中数学 来源: 题型:
【题目】某研究所开发了一种新药,测得成人注射该药后血药浓度y(微克/毫升)与给药时间x(小时)之间的若干组数据,并由此得出y与x之间的一个拟合函数y=40(0.6x﹣0.62x)(x∈[0,12]),其简图如图所示.试根据此拟合函数解决下列问题:

(1)求药峰浓度与药峰时间(精确到0.01小时),并指出血药浓度随时间的变化趋势;
(2)求血药浓度的半衰期(血药浓度从药峰浓度降到其一半所需要的时间)(精确到0.01小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴的 非负半轴为极轴建立极坐标系,曲线
轴的 非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1(-
(a>b>0)的两个焦点分别为F1(-![]() ,0)、F2(
,0)、F2(![]() ,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)已知点N的坐标为(3,2),点P的坐标为(m,n)(m≠3).过点M任作直线l与椭圆C相交于A、B两点,设直线AN、NP、BN的斜率分别为k1、k2、k3,若k1+k3=2k2,试求m,n满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中,为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com