
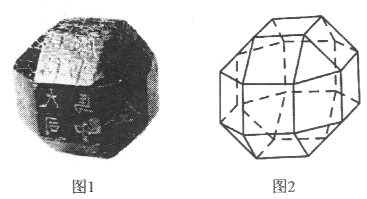
����Ŀ���й����ƾõĽ�ʯ�Ļ���ӡ���ǽ�ʯ�Ļ��Ĵ���֮һ.ӡ�ŵ���״��Ϊ�����塢�������Բ���壬���ϱ���ʱ�ڵĹ�Ա�����ŵ�ӡ����״������������������ͼ1��.�����������������ֻ��������ϵ��������Χ�ɵĶ�����.������������������ѧ�ĶԳ���.ͼ2��һ������Ϊ48�İ��������壬�������ж��㶼��ͬһ��������ı����ϣ��Ҵ���������ⳤΪ1.��ð���������������ⳤ��Ϊ_______.
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������
������![]() ��
��![]() .
.
��1����![]() ��������
��������![]() ��ͼ���һ���Գ���Ϊֱ��
��ͼ���һ���Գ���Ϊֱ��![]() ����
����![]() ��ֵ��
��ֵ��
��2������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ����������ƽ��
����λ����������ƽ��![]() ����λ�õ���ͼ������ԭ�㣬����������������
����λ�õ���ͼ������ԭ�㣬����������������![]() ��
��![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() ����֪����
����֪����![]() ������
������![]() �ϵ������������Ϊ
�ϵ������������Ϊ![]() ����
����![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=x3��3x+c��ͼ����x��ǡ�����������㣬��c=�� ��
A.��2��2
B.��9��3
C.��1��1
D.��3��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բx2+y2=1��ÿһ��ĺ����걣�ֲ���,�������Ϊԭ����2��,������C.
(1)д��C����ͨ����;
(2)��ֱ��l:2x+y-2=0��C�Ľ���ΪP1,P2,������ԭ��Ϊ����,x��������Ϊ���Ὠ��������ϵ,����߶�P1P2���е�����l��ֱ��ֱ�ߵļ����귽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ��I=��1��2��3��4��5��6��������A��B����I���Ӽ�����A![]() B=��1��3��5�������A��BΪ�������伯����������A��B�������������������伯����A��B�����У� ��
B=��1��3��5�������A��BΪ�������伯����������A��B�������������������伯����A��B�����У� ��
A. 7�� B. 8�� C. 27�� D. 28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x����x��R������f����x��=f��x����f��x��=f��2��x�����ҵ�x��[0��1]ʱ��f��x��=x3 �� �ֺ���g��x��=|xcos����x��|������h��x��=g��x����f��x���� ![]() �ϵ�������Ϊ�� ��
�ϵ�������Ϊ�� ��
A.5
B.6
C.7
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������أ������Ĺ����������ܵ������ص�Ӱ�죬��θ��ƿ��������ѳ�Ϊ������ȵ����⣬ij�������������쳧������Ͷ������ij�ͺŵĿ����������������������������۾���õ������й��������۵�ͳ�ƹ��ɣ�ÿ�������ͺſ���������![]() ����̨�������ܳɱ�Ϊ
����̨�������ܳɱ�Ϊ![]() ����Ԫ�������й̶��ɱ�Ϊ12��Ԫ������ÿ����1��̨�������ɱ�Ϊ10��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������
����Ԫ�������й̶��ɱ�Ϊ12��Ԫ������ÿ����1��̨�������ɱ�Ϊ10��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������![]() ����Ԫ������
����Ԫ������![]() ���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
��1����������![]() �Ľ���ʽ������=��������-�ܳɱ�����
�Ľ���ʽ������=��������-�ܳɱ�����
��2�������������ٰ�̨��Ʒʱ����ʹ������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���ƻ���ֲ�ƹϺ;²ˣ���ֲ���������50Ķ��Ͷ���ʽ���54��Ԫ��������ֲ�ƹϺ;²˵IJ������ɱ����ۼ����±�
�����/Ķ | ����ֲ�ɱ�/Ķ | ÿ���ۼ� | |
�ƹ� | 4�� | 1.2��Ԫ | 0.55��Ԫ |
�²� | 6�� | 0.9��Ԫ | 0.3��Ԫ |
Ϊʹһ�����ֲ������������=���������멁����ֲ�ɱ��������ô�ƹϺ;²˵���ֲ�������λ��Ķ���ֱ�Ϊ�� ��
A.50��0
B.30��20
C.20��30
D.0��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���������ijɼ�������Ķ���֮��Ĺ�ϵ��ij�о����������ȡ60�����������ʾ����飬�õ��������ݣ�
���ijɼ����� | ���ijɼ�һ�� | �ܼ� | |
�����Ķ����ϴ� | 22 | 10 | 32 |
�����Ķ���һ�� | 8 | 20 | 28 |
�ܼ� | 30 | 30 | 60 |
���������ݣ�����õ�![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() �������ٽ�ֵ��������˵����ȷ����(����)
�������ٽ�ֵ��������˵����ȷ����(����)
P(K2��k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.05 | 0.010 | 0.005 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
A. ������������û�з����㹻֤��֧�ֽ��ۡ����ijɼ�����������Ķ������йء�
B. �ڷ�����ĸ��ʲ�����0.001��ǰ���£���Ϊ���ijɼ�����������Ķ������й�
C. �ڷ�����ĸ��ʲ�����0.05��ǰ���£���Ϊ���ijɼ�����������Ķ������й�
D. �ڷ�����ĸ��ʲ�����0.005��ǰ���£���Ϊ���ijɼ�����������Ķ������й�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com