练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是，从B中摸出一个红球的概率为p．

    （1）从A中有放回地摸球，每次摸出一个，有3次摸到红球即停止．求恰好摸5次停止的概率；

    （2）若A，B两个袋子中的球数之比为，将A，B中的球装在一起后，从中摸出一个红球的概率是，求p的值．

    【答案】（1）；（2）

    【解析】

    （1）根据题意，第5次必须摸到红球，而前4次中必须恰好有两次摸到红球，计算概率得到答案.

    （2）设A中有球3k个，计算总球数和红球个数，得到，解得答案.

    （1）第5次必须摸到红球，而前4次中必须恰好有两次摸到红球，

    所求概率为.

    （2）设A中有球3k个，则其中有红球k个，则B中有球6k个，并设B中有红球x个，

    于是，，所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】镇江市长江路江边春江潮广场要设计一尊鼎型塑像（如图1），塑像总高度为12米，塑像由两部分组成，上半部分由四根垂直于水平地面的等高垂直立柱组成（立柱上凸起部分忽略不计），下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成，如图2所示．设计要求正棱台的水平横柱长度为4米，下底面边长为8米，设斜柱与地面的所成的角为．

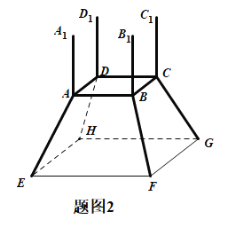
    （1）用表示塑像上半部分立柱的高度，并求的取值范围？

    （2）若该塑像上半部分立柱的造价为千元/米（立柱上凸起部分忽略不计），下半部分横柱和斜柱的造价都为2千元/米，问当为何值时，塑像总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图．则下列说法不正确的是（ ）

    A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数

    B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低

    C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天

    D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求的定义域和值域；

    （2）求的单调区间；

    （3）设的反函数为，解关于x的方程：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.

    (1)求取出的4个球均为黑球的概率.

    (2)求取出的4个球中恰有1个红球的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果执行程序框图，输入正整数，，满足，那么输出的等于（ ）．

    [Failed to download image : http://192.168.0.10:8086/QBM/2020/6/25/2492401463009280/2492946029182977/STEM/3a3c20c7c34c41528daf48813411739a.png]

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位6个员工借助互联网开展工作，每个员工上网的概率都是0.5（相互独立）．至少3人同时上网的概率为________；至少________人同时上网的概率小于0.3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双曲线C的渐近线方程为，一个焦点为F（0，﹣8），则该双曲线的标准方程为_____.已知点A（﹣6，0），若点P为C上一动点，且P点在x轴上方，当点P的位置变化时，△PAF的周长的最小值为_____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在30瓶饮料中，有3瓶已过了保质期．从这30瓶饮料中任取2瓶，则至少取到一瓶已过保质期的概率为　_________　．（结果用最简分数表示）

    查看答案和解析>>

    同步练习册答案