

分析 (1)利用向量的加法,可得结论;
(2)①证明$\overrightarrow{EG}$=$\overrightarrow{E{D}_{1}}$+$\overrightarrow{{D}_{1}G}$=$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{AC}$,即可证明结论;
②证明EG∥平面AB1C,EF∥平面AB1C,利用EF∩EG=E,即可证明平面EFG∥平面AB1C.
解答 (1)解:由题意,$\overrightarrow{D{B}_{1}}$=$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{B{A}_{1}}$=$\overrightarrow{BA}$+$\overrightarrow{A{A}_{1}}$=-$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{C{A}_{1}}$=$\overrightarrow{a}$-$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{DG}$=$\overrightarrow{DC}$+$\overrightarrow{CG}$=$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$.
(2)证明:①$\overrightarrow{EG}$=$\overrightarrow{E{D}_{1}}$+$\overrightarrow{{D}_{1}G}$=$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{AC}$,
∴EG∥AC;
②由①EG∥AC,EG?平面AB1C,AC?平面AB1C,∴EG∥平面AB1C.
同理EF∥平面AB1C.
∵EF∩EG=E,
∴平面EFG∥平面AB1C.
点评 本题考查向量知识的运用,考查线线平行,线面、面面平行,考查学生分析解决问题的能力,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
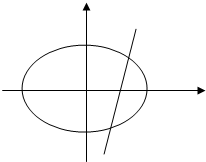 已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.
已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-2且x≠1} | B. | {x|x≥-2} | C. | {x|x≥-2或x≠1} | D. | {x|x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com