
已知圆 :
: ,
,
直线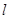 :
: ,且
,且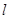 与圆
与圆 相交于
相交于 、
、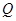 两点,点
两点,点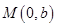 ,且
,且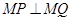 .
.
(1)当 时,求
时,求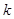 的值;
的值;
(2)当 ,求
,求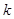 的取值范围.
的取值范围.
(1)k=1(2)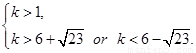
【解析】(1)因为当b=1时,M在圆C上,所以由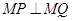 可知直线l过圆心,从而求出k.
可知直线l过圆心,从而求出k.
(2)设设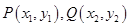 ,
, ,
,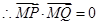
所以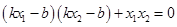 ,即
,即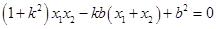 ,
,
然后直线l的方程与圆C的方程联立,消y后借助韦达定理来解决即可.
解:(1)圆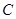 :
: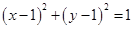 ,当
,当 时,点
时,点 在圆
在圆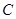 上,当且仅当直线
上,当且仅当直线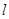 经过圆心
经过圆心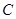 时, 满足
时, 满足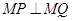 .
. 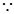 圆心
圆心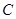 的坐标为
的坐标为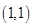 ,
,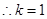 .………………………………………4分
.………………………………………4分
(2)由
消去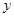 得:
得: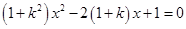 .
①…………………6分
.
①…………………6分
设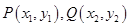 ,
, 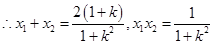 .
.
 ,
,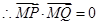 .
.
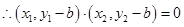 , 即
, 即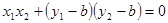 .
.
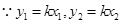 ,
,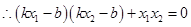 , 即
, 即
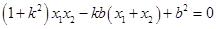 .……………………8分
.……………………8分
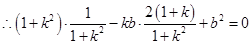 ,即
,即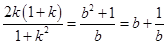 .
.
令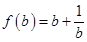 , 则. 当
, 则. 当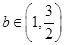 时,由对号函数知:
时,由对号函数知:
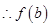 在区间
在区间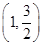 上单调递增.
上单调递增.
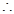 当
当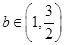 时,
时,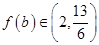 .
……………………10分
.
……………………10分
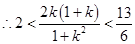 . 即
. 即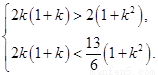
解得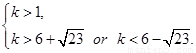 ……………12分
……………12分
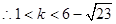 或
或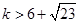 .
.
由①式得 , 解得
, 解得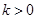 .
.
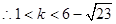 或
或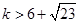 .
. 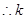 的取值范围是
的取值范围是
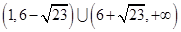 .……14分
.……14分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
|
3
| ||
| 7 |
3
| ||
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com