
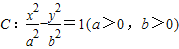 的左、右顶点分别为A、B,右焦点为F(
的左、右顶点分别为A、B,右焦点为F( ,0),
,0), ,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q.
,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q. 的取值范围.
的取值范围.
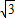 ,0),一条渐近线的方程为
,0),一条渐近线的方程为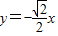 ,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;
,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;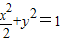 ,利用韦达定理,及
,利用韦达定理,及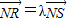 ,
,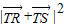 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-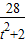 +
+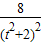 ,即可求得结论.
,即可求得结论.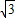 ,0),一条渐近线的方程为
,0),一条渐近线的方程为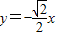 ,
,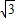 ,
,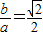
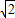 ,b=1
,b=1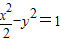 ;
;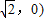 ,B(
,B(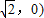
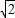 )y=y(x+
)y=y(x+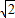 )
) )y=-y(x-
)y=-y(x-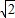 )
)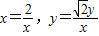
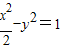
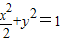
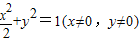 ;
;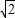 ,0),S(
,0),S(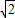 ,0),N(1,0),
,0),N(1,0),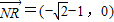 ,
,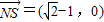
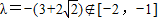
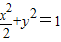 ,可得(t2+2)y2+2ty-1=0
,可得(t2+2)y2+2ty-1=0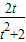 ,y1y2=-
,y1y2=-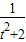
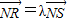 ,∴y1=λy2,∴λ=
,∴y1=λy2,∴λ=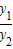 ,λ<0
,λ<0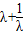 +2=
+2=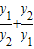 +2=
+2=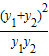 =-
=-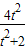
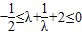
 ≤-
≤-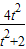 ≤0
≤0
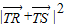 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-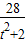 +
+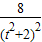
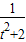 ,则n∈[
,则n∈[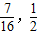 ]
]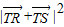 =8n2-28n+16=8(n-
=8n2-28n+16=8(n- )2-
)2-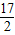
 时,
时,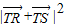 min=4;n=
min=4;n=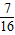 时,
时,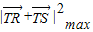 =
=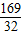
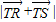 ∈[2,
∈[2,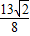 ].
].

科目:高中数学 来源:江西省09-10学年度高二下学期期末联考考试数学试题(文科) 题型:解答题
(本小题满分14分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与 交点的轨迹E的方程
交点的轨迹E的方程
(2若过点 的两条直线
的两条直线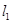 和
和 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省八校高三第一次联考理科数学卷 题型:解答题
(本小题满分 分)
分)
已知双曲线 的左、 右顶点分别为
的左、 右顶点分别为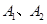 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.

(Ⅰ)求 的取值范围,并求
的取值范围,并求 的最小值;
的最小值;
(Ⅱ)记直线 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省淄博市高三第一学期期末数学理卷 题型:选择题
已知双曲线 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
,则
A、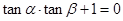 B、
B、
C、 D、
D、
查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二上学期期末考试理科数学 题型:解答题
(本小题满分12分)已知双曲线 的左、右顶点分别为
的左、右顶点分别为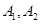 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.
(1)求直线 与
与 交点的轨迹E的方程
交点的轨迹E的方程
(2)若过点H(0, h)(h>1)的两条直线 和
和 与轨迹E都只有一个公共点,且
与轨迹E都只有一个公共点,且 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:浙江省2009-2010学年第二学期高二3月月考数学试卷 题型:选择题
已知双曲线 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
( )
,则
( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com